dp复习

Posted Sep 8, 2023

By 36 min read

状压dp

棋盘式

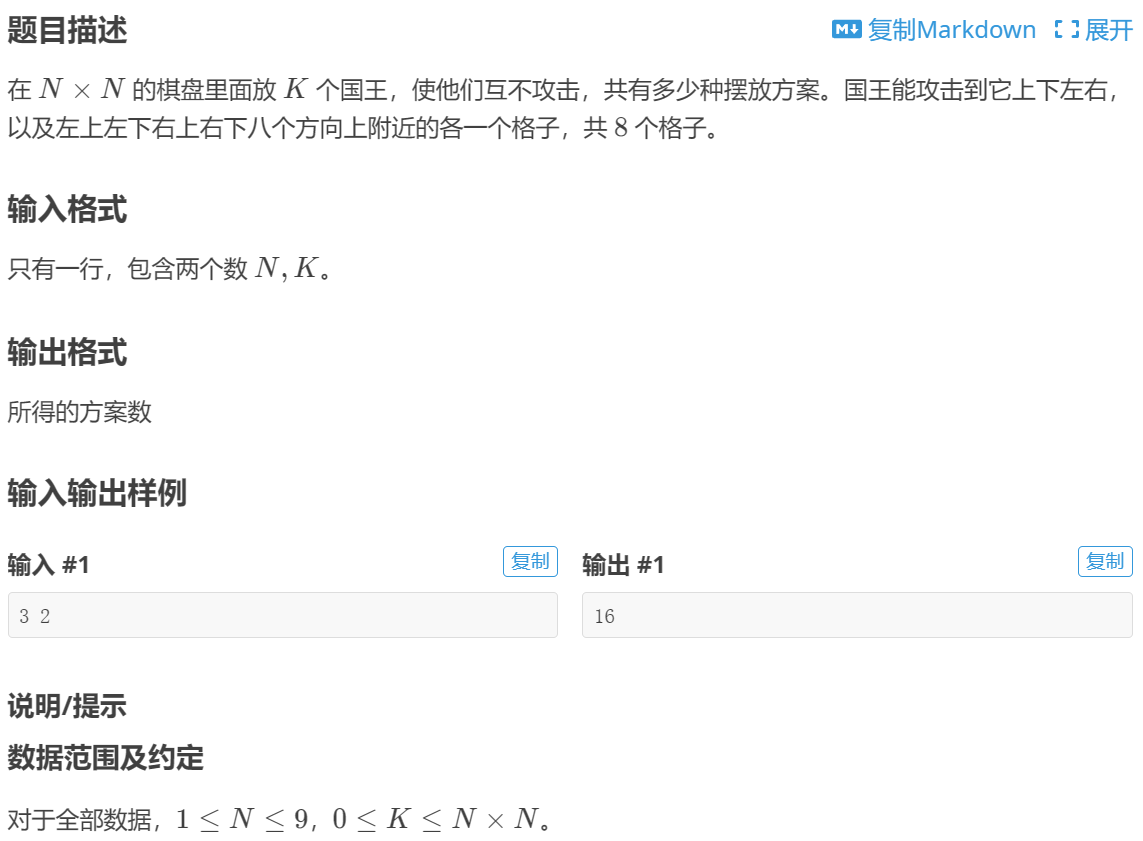
P1896互不侵犯

  
#include<bits/stdc++.h>
#define int long long
const int mod=1e9+7;
using namespace std;
const int N=110,M=10;
int cnt[1<<M];//当前状态行1的个数
vector<int> state;//存储可选行
int dp[2][M*M][1<<M];//dp[i][j][k]表示第i行选了j个国王当前状态为k的方案数
int n,m;
vector<int> head[1<<M];//可以与相应行匹配的其他行
bool check(int x){//判断可选行
    for(int i=0;i<n;i++){
        if((x>>i&1)&&(x>>i+1&1))return false;
    }
    return true;
}
int count(int x){
    int res=0;
    for(int i=0;i<n;i++)res+=(x>>i&1);
    return res;
}
void solve(){
    cin>>n>>m;
    for(int i=0;i<1<<n;i++){
        if(check(i)){
            state.push_back(i);
            cnt[i]=count(i);
        }
    }
    for(int i=0;i<state.size();i++){
        for(int j=0;j<state.size();j++){
            int a=state[i],b=state[j];
            if((a&b)==0&&check(a|b))head[i].push_back(j);
        }
    }
    dp[0][0][0]=1;
    for(int i=1;i<=n+1;i++){
        for(int j=m;j>=0;j--){
            for(int a=0;a<state.size();a++){
                for(int b:head[a]){
                    int c=cnt[state[a]];
                    if(j>=c)dp[i&1][j][a]+=dp[i-1&1][j-c][b];
                    //if(dp[i&1][j][a]!=0)cout<<i<<" "<<j<<" "<<a<<" "<<b<<" "<<dp[i&1][j][a]<<"\n";
                }
            }
        }
        memset(dp[i-1&1],0,sizeof(dp[i-1&1]));
    }
    cout<<dp[n+1&1][m][0];
}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int T=1;
    //cin>>T;
    while(T--)solve();
    return 0;
}

炮兵阵地

  
#include<bits/stdc++.h>
#define int long long
const int mod=1e9+7;
using namespace std;
const int N=110,M=11;
int g[N],cnt[1<<M];
vector<int> state;
int dp[2][1<<M][1<<M];//dp[i][j][k]表示当前状态为j，上一状态为k的能放的炮兵数
int n,m;
bool check(int x){
    for(int i=0;i<m;i++){
        if((x>>i&1)&&((x>>i+1&1)|(x>>i+2&1)))return false;
    }
    return true;
}
int count(int x){
    int res=0;
    for(int i=0;i<m;i++)res+=(x>>i&1);
    return res;
}
void solve(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=0;j<m;j++){
            char c;
            cin>>c;
            if(c=='H')g[i]+=1<<j;
        }
    }
    for(int i=0;i<1<<m;i++){
        if(check(i)){
            state.push_back(i);
            cnt[i]=count(i);
        }
    }
    for(int i=1;i<=n+2;i++){
        for(int j=0;j<state.size();j++){
            for(int k=0;k<state.size();k++){
                for(int u=0;u<state.size();u++){
                    int a=state[j],b=state[k],c=state[u];
                    if((a&c)|(b&c)|(a&c))continue;
                    if((g[i]&a)|(g[i-1]&b))continue;
                    if(i>=2&&(g[i-2]&c))continue;
                    dp[i&1][j][k]=max(dp[i&1][j][k],dp[i-1&1][k][u]+cnt[a]);
                }
            }
        }
    }
    cout<<dp[n+2&1][0][0];//到n的话需要统计所有情况，因此可以到n+2
}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int T=1;
    //cin>>T;
    while(T--)solve();
    return 0;
}

集合式

P2831愤怒的小鸟

题意：
给定多个点，问至少有多少条开口向下的抛物线能将这些点完全覆盖
思路：
预处理出 $ n^2 $ 条抛物线，将该抛物线能覆盖到的点用状压表示，然后状态转移

  
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-6;
const int N=20,M=1<<20;
int f[M];
int path[N][N],n,m;
double X[N],Y[N];
int cmp(double x,double y){
    if(fabs(x-y)<eps)return 0;
    if(x>y)return 1;
    return -1;
}
void solve(){
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>X[i]>>Y[i];
    memset(path,0,sizeof path);
    for(int i=0;i<n;i++){
        path[i][i]=1<<i;
        for(int j=0;j<n;j++){
            if(!cmp(X[i],X[j]))continue;
            double a=(Y[i]/X[i]-Y[j]/X[j])/(X[i]-X[j]);
            double b=Y[i]/X[i]-a*X[i];
            //cout<<a<<" "<<b<<"\n";
            if(a>0)continue;
            int state=0;
            for(int k=0;k<n;k++){
                double x=X[k],y=Y[k];
                if(!cmp(a*x*x+b*x,y))state+=1<<k;
            }
            path[i][j]=state;
        }
    }
    memset(f,0x3f,sizeof f);
    f[0]=0;
    for(int i=0;i+1<1<<n;i++){
        int x=0;
        for(int j=0;j<n;j++){
            if(!(i>>j&1)){
                x=j;
                break;
            }
        }
        for(int j=0;j<n;j++){
            f[i|path[x][j]]=min(f[i|path[x][j]],f[i]+1);
        }
    }
    cout<<f[(1<<n)-1]<<"\n";
}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int T=1;
    cin>>T;
    while(T--)solve();
    return 0;
}

P3869宝藏(bfs+状态压缩)

思路：
bfs第一次到达则为最小步数
记忆化搜索，每个状态下的x,y是否被搜过

  
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=40,M=1<<10;
int n,m;
bool vis[N][N][M];
int dp[N][N][M];
char a[N][N];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
struct node{
    int x,y,step,state;
};
struct MP{
    int x,y,a,b;
};
void solve(){
    cin>>n>>m;
    int sx,sy,ex,ey;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
            if(a[i][j]=='S')sx=i,sy=j;
            if(a[i][j]=='T')ex=i,ey=j;
        }
    }
    int k;
    cin>>k;
    vector<MP> b(k);
    for(int i=0;i<k;i++){
        cin>>b[i].x>>b[i].y>>b[i].a>>b[i].b;
    }
    queue<node> q;
    q.push({sx,sy,0,0});
    vis[sx][sy][0]=1;
    while(!q.empty()){
        auto [x,y,step,state]=q.front();
        q.pop();
        //cout<<x<<" "<<y<<"\n";
        if(x==ex&&y==ey){
            cout<<step<<"\n";
            return;
        }
        for(int i=0;i<4;i++){
            int tx=x+dx[i],ty=y+dy[i];
            if(tx<1||tx>n||ty<1||ty>m)continue;
            bool g=0;
            if(a[tx][ty]!='#')g=1;
            int ss=state;
            for(int j=0;j<k;j++){
                if(tx==b[j].a&&ty==b[j].b&&(state>>j&1))g^=1;
                if(tx==b[j].x&&ty==b[j].y)ss^=(1<<j);
            }
            if(g&&!vis[tx][ty][ss]){
                vis[tx][ty][ss]=1;
                q.push({tx,ty,step+1,ss});
            }
        }
    }

}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int T=1;
    //cin>>T;
    while(T--)solve();
    return 0;
}

区间dp

大致思路 $ O(n^3)$：

先枚举长度len
再枚举左端点l
右端点为r=l+len-1

枚举中间分隔点k

能量项链

思路：
断环成链，注意dp的l，r范围定义

  
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int M=1100;
ll f[M][M];
ll w[M<<1];
void solve(){
  int n;
  cin>>n;
  for(int i=1;i<=n;i++)cin>>w[i],w[i+n]=w[i];
  for(int len=1;len<=n+1;len++){
      for(int l=1;l+len-1<=2*n;l++){
          int r=l+len-1;
          for(int k=l+1;k<r;k++){
              f[l][r]=max(f[l][r],f[l][k]+f[k][r]+w[l]*w[r]*w[k]);
          }
      }
  }
  ll ans=0;
  for(int i=1;i<=2*n;i++)ans=max(ans,f[i][i+n]);
  cout<<ans;
}
signed main(){
  cin.tie(0)->sync_with_stdio(0);
  int T=1;
  //cin>>T;
  while(T--)solve();
  return 0;
}

P1040加分二叉树

注意记录每一段的根节点，最后用dfs输出前序遍历

  
#include<iostream>
using namespace std;
int n,w[35];
int f[35][35],s[35][35];
inline void dfs(int l,int r){
  if(l>r)return;
  cout<<s[l][r]<<" ";
  dfs(l,s[l][r]-1);
  dfs(s[l][r]+1,r);
}
signed main(){
  cin>>n;
  for(int i=1;i<=n;i++)cin>>w[i];
  for(int len=1;len<=n;len++){
      for(int i=1;i+len-1<=n;i++){
          int j=i+len-1;
          if(len==1)f[i][j]=w[i],s[i][j]=i;
          else{
              for(int k=i;k<=j;k++){
                  int l=(k==i?1:f[i][k-1]);
                  int r=(k==j?1:f[k+1][j]);
                  int tmp=l*r+w[k];
                  if(tmp>f[i][j]){
                      f[i][j]=tmp;
                      s[i][j]=k;
                  }
              }
          }
      }
  }
  cout<<f[1][n]<<"\n";
  dfs(1,n);
  return 0;
}

P5752棋盘分割(二维区间dp)

  
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=10,M=15;
int a[N][N],s[N][N],n;
double f[N][N][N][N][M];
double X;
double get(int x1,int y1,int x2,int y2){
  double sum=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]-X;
  return sum*sum/n;
}
double dp(int x1,int y1,int x2,int y2,int k){
  double &v=f[x1][y1][x2][y2][k];
  if(v>=0)return v;
  if(k==1)return v=get(x1,y1,x2,y2);
  v=1e9;
  for(int i=x1;i<x2;i++){
      v=min(v,dp(x1,y1,i,y2,k-1)+get(i+1,y1,x2,y2));
      v=min(v,dp(i+1,y1,x2,y2,k-1)+get(x1,y1,i,y2));
  }
  for(int i=y1;i<y2;i++){
      v=min(v,dp(x1,y1,x2,i,k-1)+get(x1,i+1,x2,y2));
      v=min(v,dp(x1,i+1,x2,y2,k-1)+get(x1,y1,x2,i));
  }
  return v;
}
void solve(){
  cin>>n;
  for(int i=1;i<=8;i++){
      for(int j=1;j<=8;j++){
          cin>>a[i][j];
          s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
      }
  }
  memset(f,-1,sizeof f);
  X=(double)s[8][8]/n;
  cout<<setprecision(3)<<fixed<<sqrt(dp(1,1,8,8,n));
}
signed main(){
  cin.tie(0)->sync_with_stdio(0);
  int T=1;
  //cin>>T;
  while(T--)solve();
  return 0;
}

P4170涂色

  
const int N=60;
string s;
int f[N][N];//f[i][j]表示区间[i,j]的方案数
/*
如果s[i]==s[j],f[i][j]=min(f[i][j-1],f[i+1][j])
否则,枚举中间节点
*/
void solve(){
  cin>>s;
  int n=s.size();
  s=" "+s;
  memset(f,0x3f,sizeof f);
  for(int i=1;i<=n;i++)f[i][i]=1;
  for(int len=2;len<=n;len++){
      for(int l=1;l+len-1<=n;l++){
          int r=l+len-1;
          if(s[l]==s[r])f[l][r]=min(f[l][r-1],f[l+1][r]);
          else{
              for(int k=l;k<r;k++)f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]);
          }
      }
  }
  cout<<f[1][n];
}

P8675搭积木(前缀和+区间dp)

思路： $ dp_{i,j,k}表示第i层,[j,k]为搭建的积木的所有方案数,则ans=\sum dp_{i,j,k} $
利用前缀和判断当前行的选中区间是否能连续
$ 假设当前第i行枚举的区间为[j,k],则第i+1行区间[x,y]满足1<=x<=j<=k<=y<=m的区间都累加上去 $
$ 直接枚举为O(n^5) ,可以再用一个前缀和优化成O(n^3) $

P1436棋盘分割

  
#include<bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int,int> PII;
const int N=10,M=15;
ll a[N][N],s[N][N],n;
ll f[N][N][N][N][M];
ll get(int x1,int y1,int x2,int y2){
  ll sum=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
  return sum*sum;
}
ll dp(int x1,int y1,int x2,int y2,int k){
  ll &v=f[x1][y1][x2][y2][k];
  if(v>=0)return v;
  if(k==1)return v=get(x1,y1,x2,y2);
  v=1e9;
  for(int i=x1;i<x2;i++){
      v=min(v,dp(x1,y1,i,y2,k-1)+get(i+1,y1,x2,y2));
      v=min(v,dp(i+1,y1,x2,y2,k-1)+get(x1,y1,i,y2));
  }
  for(int i=y1;i<y2;i++){
      v=min(v,dp(x1,y1,x2,i,k-1)+get(x1,i+1,x2,y2));
      v=min(v,dp(x1,i+1,x2,y2,k-1)+get(x1,y1,x2,i));
  }
  return v;
}
void solve(){
  cin>>n;
  for(int i=1;i<=8;i++){
      for(int j=1;j<=8;j++){
          cin>>a[i][j];
          s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
      }
  }
  memset(f,-1,sizeof f);
  cout<<dp(1,1,8,8,n);
}
signed main(){
  cin.tie(0)->sync_with_stdio(0);
  int T=1;
  //cin>>T;
  while(T--)solve();
  return 0;
}

树形dp

树的最长路径

两次dfs做法(只适用于无负权边)

从任意点出发找最长路的点a，再从a出发找最长b,ab即为所求

  
void solve(){
  int n;
  cin>>n;
  vector<int> adj[n+1],dis(n+1,-1);
  for(int i=1;i<n;i++){
      int u,v;
      cin>>u>>v;
      adj[u].push_back(v);
      adj[v].push_back(u);
  }
  queue<int> q;
  q.push(1);
  dis[1]=0;
  while(!q.empty()){
      auto u=q.front();
      q.pop();
      for(auto v:adj[u]){
          if(dis[v]==-1){
              dis[v]=dis[u]+1;
              q.push(v);
          }
      }
  }
  int x=0,mx=-1;
  for(int i=1;i<=n;i++){
      if(dis[i]>mx){
          mx=dis[i];
          x=i;
      }
  }
  for(int i=1;i<=n;i++)dis[i]=-1;
  dis[x]=0;
  q.push(x);
  while(!q.empty()){
      auto u=q.front();
      q.pop();
      for(auto v:adj[u]){
          if(dis[v]==-1){
              dis[v]=dis[u]+1;
              q.push(v);
          }
      }
  }
  mx=0;
  for(int i=1;i<=n;i++){
      mx=max(mx,dis[i]);
  }
  cout<<mx;
}

树形dp(最大次大值更新)

枚举到当前节点时，直径一定是子分支的两个最大值连在一起作为直径

  
int dfs(int u,int fa){
  int d1=0,d2=0;
  for(auto v:adj[u]){
      if(v!=fa){
          int d=dfs(v,u)+w;
          if(d>=d1){
              d2=d1;
              d1=d;
          }
          else if(d>=d2)d2=d;
      }
  }
  ans=max(ans,d1+d2);
  return d1;
}

树的最长路径的应用

SP6717 two paths(最水的黑题)/弱化版:CF14D two paths

题意：
在树中找出两条不相交的路径，最大化二者长度的乘积思路：

首先，按照最大次大值更新的方法可以更新出每棵子树的能找到的最长路径

然后就是要找除子树之外的另一条最长路径

可以发现对于一个确定的u，每个v的子树外的点是不一样的，这就导致每次子树外的另一条路径不是定值
思考从下往上找时的思路，是更新了当前节点的最长后，返回当前点的最长深度并对所有路径的最长值取max即g[u]=max(g[u],g[v])
因此对于一个确定的v,应该将已经找到的最长路径长度mx和到每个根节点的长度up作为参数往下传
那么对于up有可能是到根节点，也有可能是到令一个子节点的最底端
因此可以先预处理，从每一个子节点的深度和u往上走的最长深度中找最大的三个值d1,d2,d3,和他们所属边的第一个节点son1,son2,son3
$ if (v=son_1):MX=max(mx,d_2+d_3),UP=d_2 $
$ if (v=son_2):MX=max(mx,d_1+d_3),UP=d_1 $

$ else: MX=max(d_1+d_2),UP=d_1 $

  
void solve(){
  int n;
  cin>>n;
  vector<int> adj[n+1],dep(n+1),g(n+1),f(n+1);
  for(int i=1;i<n;i++){
  int u,v;
  cin>>u>>v;
  adj[u].push_back(v);
  adj[v].push_back(u);
  }
  function<int(int,int)> dfs_u=[&](int u,int fa){
  int d1=0,d2=0;
  for(auto v:adj[u]){
      if(v==fa)continue;
      int d=dfs_u(v,u)+1;
      if(d>=d1)d2=d1,d1=d;
      else if(d>=d2)d2=d;
      dep[u]=max(dep[u],dep[v]+1);
      g[u]=max(g[u],g[v]);
  }
  g[u]=max(g[u],d1+d2);
  return d1;
  };
  ll ans=0;
  function<void(int,int,int,int)> dfs_d=[&](int u,int fa,int up,int mx){
  int d1=up,son1=fa,d2=0,son2=0,d3=0,son3=0;
  for(auto v:adj[u]){
      if(v==fa)continue;
      int d=dep[v]+1;
      if(d>=d1){
          d3=d2;
          son3=son2;
          d2=d1;
          son2=son1;
          d1=d;
          son1=v;
      }
      else if(d>=d2){
          d3=d2;
          son3=son2;
          d2=d;
          son2=v;
      }
      else if(d>=d3){
          d3=d;
          son3=v;
      }
  }
  for(auto v:adj[u]){
      if(v==fa)continue;
      ll MX,UP;
      if(son1==v){
          MX=max(mx,d2+d3);
          UP=d2;
      }
      else if(son2==v){
          MX=max(mx,d1+d3);
          UP=d1;
      }
      else{
          MX=max(mx,d1+d2);
          UP=d1;
      }
      ans=max(ans,MX*g[v]);
      dfs_d(v,u,UP+1,MX);
  }
  };
  dfs_u(1,0);
  dfs_d(1,0,0,0);
  cout<<ans<<"\n";
}

数位dp

技巧

求 $ [X,Y] $ 满足的数,则 $ f(Y)-f(X-1) $
用树的方式考虑(迭代写法)

记忆化搜索

迭代写法

windy数

题意：
不含前导0且数位之间大于等于2的数

  
#include<bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int,int> PII;
ll f[15][10];
void init(){//初始化f[i][j]表示第i位为j的数位之间大于等于2的数(含有前导零)
  for(int i=0;i<10;i++){
      f[1][i]=1;
  }
  for(int i=2;i<=10;i++){
      for(int j=0;j<=9;j++){
          for(int k=0;k<=9;k++){
              if(abs(j-k)>=2){
                  f[i][j]+=f[i-1][k];
              }
          }
      }
  }
}
int dp(int n){
  if(!n)return 0;
  vector<int> nums;
  while(n)nums.push_back(n%10),n/=10;
  int res=0,last=-2;
  for(int i=nums.size()-1;i>=0;i--){//最高位不为0
      int x=nums[i];
      for(int j= (i==nums.size()-1);j<x;j++){
          if(abs(last-j)>=2)res+=f[i+1][j];
      }
      if(abs(last-x)<2)break;
      last=x;
      if(!i)res++;
  }
  for(int i=1;i<nums.size();i++){//最高位为0
      for(int j=1;j<=9;j++){
          res+=f[i][j];
      }
  }
  return res;
}
void solve(){
  init();
  int l,r;
  cin>>l>>r;
  cout<<dp(r)-dp(l-1);
}
signed main(){
  cin.tie(0)->sync_with_stdio(0);
  int T=1;
  //cin>>T;
  while(T--)solve();
  return 0;
}

恨7不成妻

```c++ #include #include

using namespace std;

typedef long long ll; const int N = 20; const ll P = 1e9+7;

//需要满足三个性质。 //1.不含7. //2.各位数字之和模7不为0.an-1+…+a0%7!=0. //3.该数模7不为0.an-1*pow(10,n-1)+…+a0+pow(10,0)%7!=0

struct F{ ll s0,s1,s2;//s0为符合要求的数。s1为符合要求的数1次方之和，s2为符合要求的数的2次方之和。 }f[N][10][7][7];//f[i][j][k][u]表示总共有i位数且最高位是j，该数值模7为k，各位数数字之和模7为u的所有数的s0,s1,s2. //进行初始化。 int t;//测试数。 ll l,r; ll power7[N],power9[N];//power7[i]存储10^i余7的余数，power9[i]存储10^i余P的余数。 ll mod(ll x,ll y){ return (x%y+y)%y; } void init(){ //确定初始值，位数为1的情况。 for(int j=0;j<10;j++){ if(j==7)continue; //根据性质排除不符合要求的。 F &v=f[1][j][j%7][j%7];//这里用引用减少代码量。 v.s0++; v.s1+=j; v.s2+=jj; } ll power = 10;//辅助作用，表示10的i-1次方。 for(int i=2;i<N;i++,power=10){ for(int j=0;j<10;j++){ if(j==7)continue;//排除不符合要求的数。 for(int k=0;k<7;k++){ for(int u=0;u<7;u++){ for(int q=0;q<10;q++){ //枚举i-1的最高位。 if(q==7)continue; F &x=f[i][j][k][u],y=f[i-1][q][mod(k-j(power%7),7)][mod(u-j,7)]; //s0,s1,s2都是通过公式就算得到。 x.s0=mod(x.s0+y.s0,P); x.s1=mod(x.s1+1LLj%P(power%P)%Py.s0%P+y.s1,P); x.s2=mod(x.s2+ 1LLj%Py.s0%P(power%P)%Pj%P(power%P)%P+ 1LLy.s1%P2%Pj%P(power%P)%P+y.s2,P); } } } } } //这里处理为了方便以及降低时间复杂度。 power7[0]=1,power9[0]=1; for(int i=1;i<N;i++){ power7[i]=power7[i-1]10%7; power9[i]=power9[i-1]*10%P; } } F get(int i,int j,int k,int u){ //因为f[i][j][k][u]是本身模7等于k，且各位数之和模7等于u的，所以我们需要找出符合条件的集合。 ll s0=0,s1=0,s2=0; for(int x=0;x<7;x++){ for(int y=0;y<7;y++){ if(x==k||y==u)continue; F v=f[i][j][x][y]; s0=mod(s0+v.s0,P); s1=mod(s1+v.s1,P); s2=mod(s2+v.s2,P); } } return {s0,s1,s2}; } ll dp(ll n){ if(!n)return 0;//0的平方和为0. vector a; ll temp=n%P;//备份一个n，供后面判断n使用。 while(n)a.push_back(n%10),n/=10; ll last_a=0,last_b=0;//这里我们需要存储前缀的本身值和前缀的个位数之和。 ll ans=0;//答案。 for(int i=a.size()-1;i>=0;i--){ int x=a[i]; for(int j=0;j<x;j++){ //走左分支。 if(j==7)continue; //我们需要将符合条件的数筛出来，这里要用到一个get函数。 //求得本身模7不等于a，并且各位数之和模7不等b的集合，此时就可以使用预处理出来的结构体 int k=mod(-last_a*power7[i+1],7),u=mod(-last_b,7); F v=get(i+1,j,k,u); //cout<<v.s0<<" "<<v.s1<<" "<<v.s2<<endl; //根据公式求解s2. //j就是last_a. ans=mod(ans+ 1LL*(last_a%P)*(last_a%P)%P*(power9[i+1]%P)%P*(power9[i+1]%P)%P*v.s0%P+ 1LL*2*last_a%P*(power9[i+1]%P)%P*v.s1%P+ v.s2,P); //cout<<ans<<endl; } //判断x。 if(x==7)break; //走右分支更新。 last_a=last_a*10+x; last_b+=x; //判断自己本身是否符合要求。 if(!i&&last_a%7&&last_b%7){ ans=mod(ans+temp*temp%P,P); } } return ans; } int main(){ init(); cin>>t; while(t--){ cin>>l>>r; cout<<mod(dp(r)-dp(l-1),P)<<endl; } return 0; }

## 记忆化搜索(套路)
时间复杂度：  
定义的状态数*10(10为枚举0-9)  
* pos: 当前数位
* limit: 为`true`为从`0-nums[pos]`,为`false`为从`0-9`  
* last: 上一位,往往出现于数位之间有关联的
* lead: 前导零  
    有前导零的情况？
    * 统计0的出现次数
    * 相邻数字的差值
    * 以最高位为起点确定的奇偶位
* r: 表示整个数前缀取模某个数`m`的余数  
    * 该参数一般会用在：约束中出现了能被整除  
    * 当然也可以拓展为数位和取模的结果
* st: 用于状态压缩对一个集合的数在数位上的出现次数的奇偶性有要求时，其二进制形式就可以表示每个数出现的奇偶性

### P2602数字计数
求区间内0-9出现的次数
```c++
int f[20][20];
vector<int> nums;
int dfs(int pos,int sum,int d,bool limit,bool lead){
    if(!pos)return sum;
    if(!limit&&!lead&&~f[pos][sum])return f[pos][sum];
    int up=limit?nums[pos-1]:9;
    int ans=0;
    for(int i=0;i<=up;i++){
        if(lead)ans+=dfs(pos-1,sum+(i==d&&d),d,limit&&i==up,lead&&i==0);
        else ans+=dfs(pos-1,sum+(i==d),d,limit&&i==up,0);
    }
    if(!limit&&!lead)f[pos][sum]=ans;
    return ans;
}
int dp(int n,int d){
    nums.clear();
    memset(f,-1,sizeof f);
    while(n)nums.push_back(n%10),n/=10;
    return dfs(nums.size(),0,d,1,1);
}
void solve(){
    int l,r;
    cin>>l>>r;
    for(int i=0;i<=9;i++){
        cout<<dp(r,i)-dp(l-1,i)<<" ";
    }
}

P4999烦人的数学作业

求区间内所有数位和

  
int f[20][200];
vector<int> nums;
int MOD(int x,int y){
    return (x%y+y)%y;
}
int dfs(int pos,int sum,bool limit){
    if(!pos)return sum;
    if(!limit&&~f[pos][sum])return f[pos][sum];
    int up=limit?nums[pos-1]:9;
    int ans=0;
    for(int i=0;i<=up;i++){
        ans=MOD(ans+dfs(pos-1,sum+i,limit&&i==up),mod);
    }
    if(!limit)f[pos][sum]=ans;
    return ans;
}
int dp(int n){
    nums.clear();
    memset(f,-1,sizeof f);
    while(n)nums.push_back(n%10),n/=10;
    return dfs(nums.size(),0,1);
}
void solve(){
    int l,r;
    cin>>l>>r;
    cout<<MOD(dp(r)-dp(l-1),mod)<<"\n";
}

P2657windy数

  
int f[15][10];
vector<int> nums;
int dfs(int pos,int last,bool limit,bool lead){
    if(!pos)return 1;
    if(!limit&&!lead&&~f[pos][last])return f[pos][last];//必须是没限制
    int up=limit?nums[pos-1]:9;//上限
    int res=0;
    for(int i=0;i<=up;i++){
        if(lead){//有前导0
            res=res+dfs(pos-1,i,limit&&i==up,lead&&i==0);
        }
        else{
            if(abs(last-i)<2)continue;
            res=res+dfs(pos-1,i,limit&&i==up,0);
        }
    }
    if(!limit&&!lead)f[pos][last]=res;
    return res;
}
int dp(int n){
    nums.clear();
    memset(f,-1,sizeof f);
    while(n)nums.push_back(n%10),n/=10;
    return dfs(nums.size(),-2,1,1);
}
void solve(){
    int l,r;
    cin>>l>>r;
    cout<<dp(r)-dp(l-1);
}

P4317花神的数论题(二进制数位dp)

$ 定义sum(i)为i在二进制下1的个数，求 \prod_{i=0}^{N}sum(i) $

  
int dfs(int pos,int cnt,bool limit){
    if(!pos)return max(cnt,1);
    if(!limit&&~f[pos][cnt])return f[pos][cnt];
    int up=limit?nums[pos-1]:1;
    int res=1;
    for(int i=0;i<=up;i++){
        res=(res%mod*dfs(pos-1,cnt+i,limit&&i==up)%mod)%mod;
    }
    if(!limit)f[pos][cnt]=res;
    return res;
}
int dp(ll n){
    nums.clear();
    memset(f,-1,sizeof f);
    while(n)nums.push_back(n%2),n/=2;
    return dfs(nums.size(),0,1);
}   
void solve(){
    ll n;
    cin>>n;
    cout<<dp(n)<<"\n";
}

P6218[USACO06NOV]Round Numbers S(二进制数位dp)

求区间内二进制下，0个数大于等于1的数量
定义f[pos][cnt0][cnt1]表示当前位置选到当前位置有cnt0个0，cnt1个1的总数量

注意前导零

  
int f[65][65][65];
vector<int> nums;
int dfs(int pos,int cnt0,int cnt1,bool limit,bool lead){
  if(!pos)return cnt0>=cnt1;
  if(!limit&&!lead&&~f[pos][cnt0][cnt1])return f[pos][cnt0][cnt1];
  int up=limit?nums[pos-1]:1;
  int res=0;
  for(int i=0;i<=up;i++){
      if(lead){
          if(i==0)res+=dfs(pos-1,cnt0,cnt1,limit&&i==up,lead);
          else res+=dfs(pos-1,cnt0,cnt1+1,limit&&i==up,0);
      }
      else{
          res+=dfs(pos-1,cnt0+(i==0),cnt1+(i==1),limit&&i==up,0);
      }
  }
  if(!limit&&!lead)f[pos][cnt0][cnt1]=res;
  return res;
}
int dp(ll n){
  nums.clear();
  memset(f,-1,sizeof f);
  while(n)nums.push_back(n%2),n/=2;
  return dfs(nums.size(),0,0,1,1);
}   
void solve(){
  ll l,r;
  cin>>l>>r;
  cout<<dp(r)-dp(l-1)<<"\n";
}

CF628D Magic Numbers

l,r范围很大，需要用字符串读入，此时使用l-1可能会产生退位(要写高精减),因此减去dp(l)然后单独判断l即可

  
int f[2010][2010],m,d;
vector<int> nums;
int MOD(int x,int y=mod){
  return (x%y+y)%y;
}
int dfs(int pos,int sum,bool limit){
  if(!pos)return sum==0;
  if(!limit&&~f[pos][sum])return f[pos][sum];
  int up=limit?nums[pos-1]:9;
  int res=0;
  bool g=(nums.size()-pos+1)&1;
  for(int i=0;i<=up;i++){
      if(g){
          if(i==d)continue;
          res=MOD(dfs(pos-1,(sum*10%m+i)%m,limit&&i==up)+res);
      }
      else{
          if(i!=d)continue;
          res=MOD(dfs(pos-1,(sum*10%m+i)%m,limit&&i==up)+res);
      }
  }
  if(!limit)f[pos][sum]=res;
  return res;
}
int dp(string n){
  nums.clear();
  memset(f,-1,sizeof f);
  for(auto c:n)nums.push_back(c-'0');
  reverse(nums.begin(),nums.end());
  return dfs(nums.size(),0,1);
}
bool check(string n){
  int sum=0;
  for(int i=0;i<n.size();i++){
      if(i%2==1&&n[i]-'0'!=d)return false;
      if(i%2==0&&n[i]-'0'==d)return false;
      sum=((sum*10)%m+n[i]-'0')%m;
  }
  return sum==0;
}   
void solve(){
  cin>>m>>d;
  string l,r;
  cin>>l>>r;
  cout<<MOD(MOD(dp(r)-dp(l))+check(l))<<"\n";
}

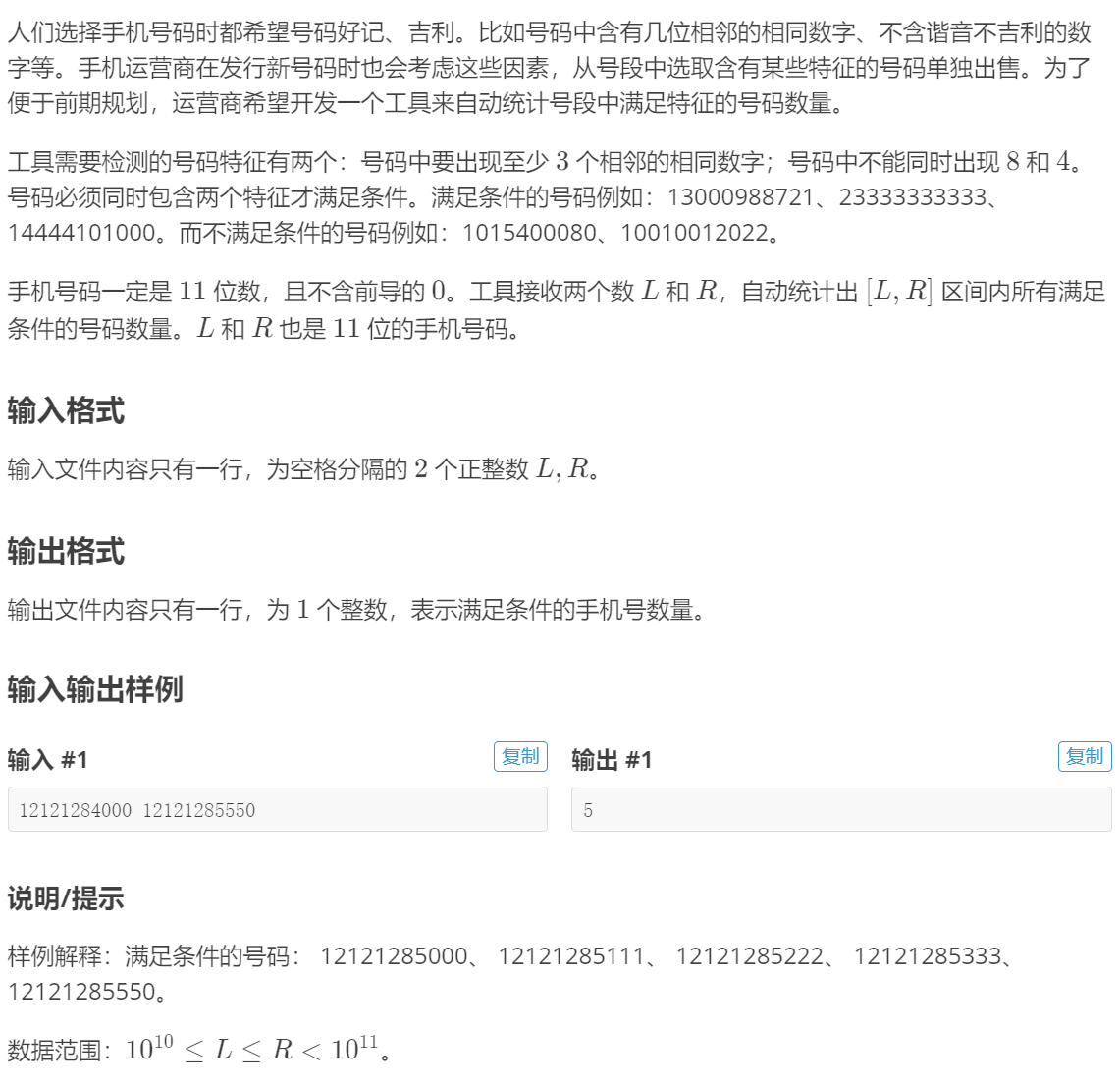
P4124 [CQOI2016]手机号码

注意：dp(1e10-1)=0要特判，最高位从1开始

  
vector<int> nums;
ll f[15][10][10][2][2][2];//f[pos][last1][last2][same][have4][have8]
ll dfs(int pos,int last1,int last2,bool have4,bool have8,bool same,bool limit){
  if(!pos)return same&&!(have4&&have8);
  auto &v=f[pos][last1][last2][same][have4][have8];
  if(!limit&&~v)return v;
  int up=limit?nums[pos-1]:9;
  int down=pos==nums.size()?1:0;//首位不能为0
  ll res=0;
  for(int i=down;i<=up;i++){
      bool tmp=same||(i==last1&&i==last2);//更新same值
      if(i==4){
          if(have8)continue;
          res+=dfs(pos-1,i,last1,1,0,tmp,limit&&i==up);
          continue;
      }
      if(i==8){
          if(have4)continue;
          res+=dfs(pos-1,i,last1,0,1,tmp,limit&&i==up);
          continue;
      }
      res+=dfs(pos-1,i,last1,have4,have8,tmp,limit&&i==up);
  }
  if(!limit)v=res;
  return res;
}
ll dp(ll n){
  if(n<1e10)return 0;
  nums.clear();
  memset(f,-1,sizeof f);
  while(n)nums.push_back(n%10),n/=10;
  return dfs(nums.size(),10,10,0,0,0,1);
} 
void solve(){
  ll l,r;
  cin>>l>>r;
  cout<<dp(r)-dp(l-1)<<"\n";
}

CF855E(数位dp+状态压缩)

求区间内[l,r]转成b进制数时数位均出现偶数次

注意数组f多建一维表示进制数，在多测时重复使用，否则tle(f数组只用memset一次)

  
vector<int> nums;
int b;
ll f[20][65][1<<10];//f[b][pos][state]表示b进制下，位置为pos，状态为state的个数
ll dfs(int pos,int state,bool limit,bool lead){
  if(!pos)return state==0&&!lead;
  if(!limit&&!lead&&~f[b][pos][state])return f[b][pos][state];
  int up=limit?nums[pos-1]:b-1;
  ll res=0;
  for(int i=0;i<=up;i++){
      if(lead){
          if(i==0)res+=dfs(pos-1,state,limit&&i==up,1);
          else res+=dfs(pos-1,state^(1<<i),limit&&i==up,0);
      }
      else res+=dfs(pos-1,state^(1<<i),limit&&i==up,0);
  }
  if(!limit&&!lead)f[b][pos][state]=res;
  return res;
}
ll dp(ll n){
  nums.clear();
  while(n)nums.push_back(n%b),n/=b;
  return dfs(nums.size(),0,1,1);
} 
void solve(){
  ll l,r;
  cin>>b>>l>>r;
  cout<<dp(r)-dp(l-1)<<"\n";
}
signed main(){
  cin.tie(0)->sync_with_stdio(0);
  int T=1;
  memset(f,-1,sizeof f);
  cin>>T;
  while(T--)solve();
  return 0;
}

P3413萌数

判断区间内有大于等于2的回文串的数的个数

注意：当仍然是前导0时，当前填的数依然为10，否则010就是合法数

  
ll f[1010][15][15][2];//f[pos][last1][last2][have]:当前位置，上一个数为last1，上上个数为last2，是否为回文串
ll MOD(ll x,ll y=mod){
  return (x%y+y)%y;
}
ll dfs(int pos,int last1,int last2,bool have,bool limit,bool lead){
  if(!pos)return have;
  auto &v=f[pos][last1][last2][have];
  if(!limit&&!lead&&~v)return v;
  int up=limit?nums[pos-1]:9;
  ll res=0;
  for(int i=0;i<=up;i++){
      bool tmp=have||i==last1||i==last2;
      if(lead){
          if(i==0){
              res=MOD(res+dfs(pos-1,10,last1,0,limit&&i==up,1));
          }
          else res=MOD(res+dfs(pos-1,i,last1,0,limit&&i==up,0));
      }
      else res=MOD(res+dfs(pos-1,i,last1,tmp,limit&&i==up,0));
  }
  if(!limit&&!lead)v=res;
  return res;
}
ll dp(string n){
  nums.clear();
  for(auto c:n)nums.push_back(c-'0');
  reverse(nums.begin(),nums.end());
  return dfs(nums.size(),10,10,0,1,1);
}
bool check(string s){
  for(int i=1;i<s.size();i++){
      if(s[i]==s[i-1])return true;
      if(i>=2&&s[i]==s[i-2])return true;
  }
  return false;
}
void solve(){
  string l,r;
  cin>>l>>r;
  memset(f,-1,sizeof f);
  cout<<MOD(MOD(dp(r)-dp(l))+check(l))<<"\n";
}

斜率优化dp

P5785任务安排

题目描述

机器上有 $n$ 个需要处理的任务，它们构成了一个序列。这些任务被标号为 $1$ 到 $n$，因此序列的排列为 $1 , 2 , 3 \cdots n$。这 $n$ 个任务被分成若干批，每批包含相邻的若干任务。从时刻 $0$ 开始，这些任务被分批加工，第 $i$ 个任务单独完成所需的时间是 $T_i$。在每批任务开始前，机器需要启动时间 $s$，而完成这批任务所需的时间是各个任务需要时间的总和。

注意，同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 $C_i$。

请确定一个分组方案，使得总费用最小。

输入格式

第一行一个整数 $n$。第二行一个整数 $s$。

接下来 $n$ 行，每行有一对整数，分别为 $T_i$ 和 $C_i$，表示第 $i$ 个任务单独完成所需的时间是 $T_i$ 及其费用系数 $C_i$。

输出格式

一行，一个整数，表示最小的总费用。

样例 #1

样例输入 #1

样例输出 #1

153

提示

对于 $100\%$ 数据，$1 \le n \le 3 \times 10^5$，$1 \le s \le 2^8$，$ \left| T_i \right| \le 2^8$，$0 \le C_i \le 2^8$。
思路：
dp方程：
$ f_i =min(f_j+sumt_i \cdot (sumc_i-sumc_j)+s \cdot (sumc_N-sumc_j))$
整理得： $ f_j=(sumt_i+s) \cdot sumc_j +f_i-sumt_i \cdot sumc_j-s \cdot sumc_N $
把 $ f_j $ 换成y, $ sumc_j $ 换成x,可转换成y=kx+b,对于一个确定的i有一个固定的斜率k且k>0,只需b尽可能小

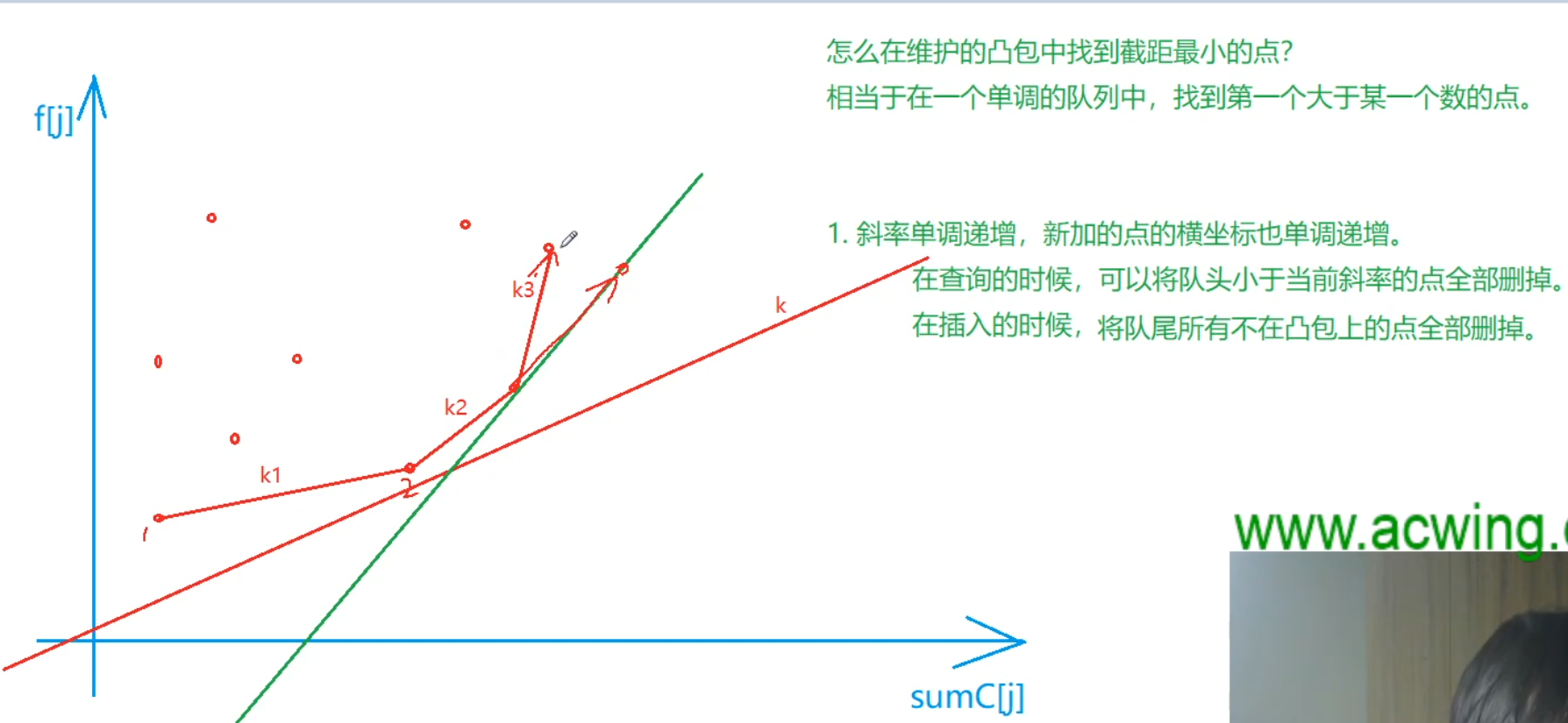
只需维护上述图片的凸包即可(利用单调队列维护)
当前斜率单调递增

将队头小于当前斜率的点删除,即$ \frac{f_{hh+1}-f_{hh}}{c_{hh+1}-c_{hh}}<=t_i+s $的点删除

单调增，即删除队尾$ \frac{f_{tt}-f_{tt-1}}{c_{tt}-c_{tt-1}}>=\frac{f_i-f_{tt}}{c_i-c_{tt}} $的点

  
#include<bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int,int> PII;
const int INF=0x3f3f3f3f;
const int mod=1e9+7;
const int N=300010;
ll f[N],t[N],c[N];
int q[N];
int n,s;
void solve(){
  cin>>n>>s;
  for(int i=1;i<=n;i++){
      cin>>t[i]>>c[i];
      t[i]+=t[i-1];
      c[i]+=c[i-1];
  }
  memset(f,0x3f,sizeof f);
  f[0]=0;
  int hh=0,tt=0;//队列
  //解释：tt=0是因为初始队列有一个元素0，是hh<tt而不是hh<=tt是因为要保证队列内值少有两个点
  for(int i=1;i<=n;i++){
      while(hh<tt&&f[q[hh+1]]-f[q[hh]]<=(t[i]+s)*(c[q[hh+1]]-c[q[hh]]))hh++;
      int j=q[hh];
      f[i]=f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j]);
      while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]]))tt--;
      q[++tt]=i;
  }
  cout<<f[n];
}
signed main(){
  cin.tie(0)->sync_with_stdio(0);
  int T=1;
  //cin>>T;
  while(T--)solve();
  return 0;
}

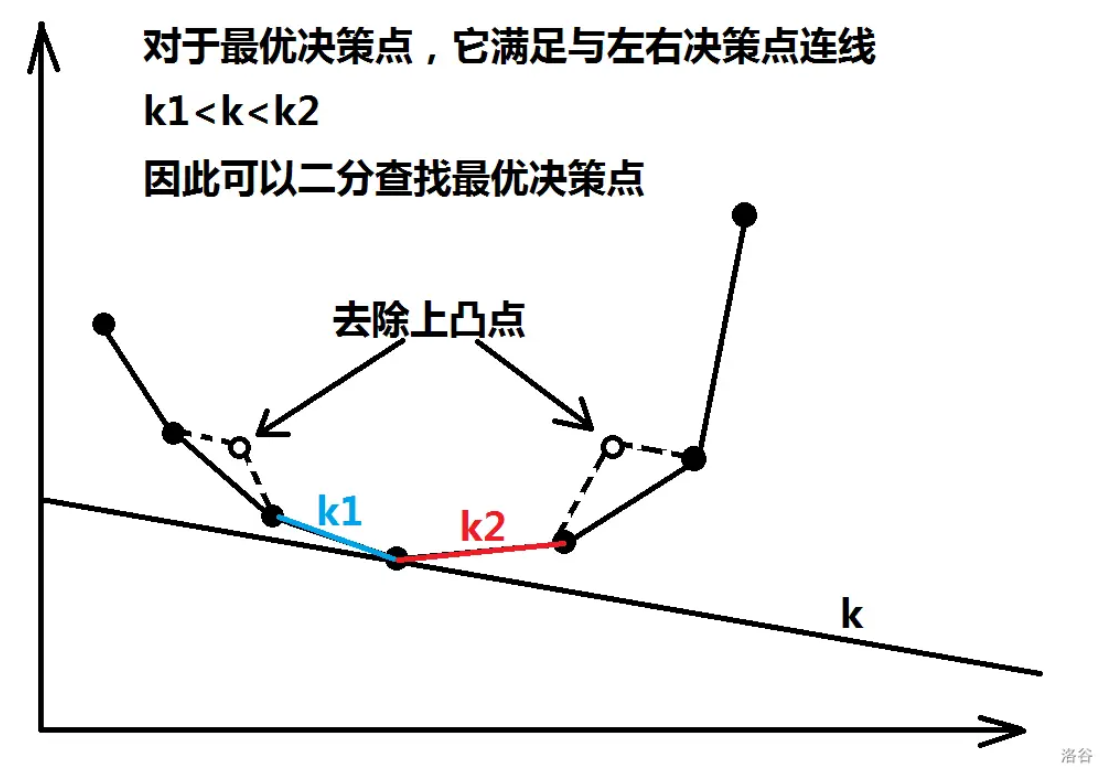
上面代码只能过掉t>0的情况，当t<0时斜率可能为负

斜率不再具有单调性，但横坐标仍具有单调性
查询的时候二分查找
删除时删去不是凸包的点

  
#include<bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int,int> PII;
const int INF=0x3f3f3f3f;
const int mod=1e9+7;
const int N=300010;
ll f[N],t[N],c[N];
int q[N];
int n,s;
void solve(){
    cin>>n>>s;
    for(int i=1;i<=n;i++){
        cin>>t[i]>>c[i];
        t[i]+=t[i-1];
        c[i]+=c[i-1];
    }
    memset(f,0x3f,sizeof f);
    f[0]=0;
    int hh=0,tt=0;//队列
    //解释：tt=0是因为初始队列有一个元素0，是hh<tt而不是hh<=tt是因为要保证队列内值少有两个点
    for(int i=1;i<=n;i++){
        int l=hh,r=tt;
        while(l<r){
            int mid=l+r>>1;
            if(f[q[mid+1]]-f[q[mid]]>(t[i]+s)*(c[q[mid+1]]-c[q[mid]]))r=mid;
            else l=mid+1;
        }
        int j=q[r];
        f[i]=f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j]);
        while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]]))tt--;
        q[++tt]=i;
    }
    cout<<f[n];
}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int T=1;
    //cin>>T;
    while(T--)solve();
    return 0;
}

P4027货币兑换

。。。。待补

CF311B 小猫铲屎

分析可得以下式子：
$ f_{j,i}=min(f_{j-1,k}+a_i(i-k)-(s_i-s_k)) $
当j,i均固定时,整理得：
$ f_{j-1,k}+s_k=a_ik+f_{j,i}+s_i-a_i*i $为 $ f_{j-1,k}+s_k $关于k的函数斜率a[i]单调递增，因此可以O(n)解决(j固定的情况下)
与第一种情况类似：

  
#include<bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int,int> PII;
const int INF=0x3f3f3f3f;
const int mod=1e9+7;
const int P=110,N=100010;
ll f[P][N],a[N],d[N],h[N],s[N];
int q[N];
int n,m,p;
ll get_y(int j,int k){
    return f[j-1][k]+s[k];
}
void solve(){
    cin>>n>>m>>p;
    for(int i=2;i<=n;i++)cin>>d[i],d[i]+=d[i-1];
    for(int i=1;i<=m;i++){
        int h,t;
        cin>>h>>t;
        a[i]=t-d[h];
    }
    sort(a+1,a+m+1);
    for(int i=1;i<=m;i++)s[i]=s[i-1]+a[i];
    memset(f,0x3f,sizeof f);
    for(int i=0;i<=p;i++)f[i][0]=0;
    for(int j=1;j<=p;j++){
        int hh=0,tt=0;
        q[0]=0;
        for(int i=1;i<=m;i++){
            while(hh<tt&&(get_y(j,q[hh+1])-get_y(j,q[hh]))<=a[i]*(q[hh+1]-q[hh]))hh++;
            int k=q[hh];
            f[j][i]=f[j-1][k]+a[i]*(i-k)-(s[i]-s[k]);
            while(hh<tt&&(get_y(j,q[tt])-get_y(j,q[tt-1]))*(i-q[tt])>=(get_y(j,i)-get_y(j,q[tt]))*(q[tt]-q[tt-1]))tt--;
            q[++tt]=i;
        }
    }
    cout<<f[p][m];
}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int T=1;
    //cin>>T;
    while(T--)solve();
    return 0;
}

总结

写出dp方程，一般来说，需要O(n^2)的复杂度来遍历前面的状态
将j与i互换，变与不变列出y=kx+b的形式
实际为维护一个凸包;
- 若斜率大于0且单调递增,则可以每次将队头小于斜率的弹出
- 否则，需要二分寻找第一个大于的斜率

概率dp,期望dp

期望

$ X=x1+x2+… $
$ E(X)=E(x1)+E(x2)+…. $

[国家集训队] 单选错位

题目描述

gx 和 lc 去参加 noip 初赛，其中有一种题型叫单项选择题，顾名思义，只有一个选项是正确答案。

试卷上共有 $n$ 道单选题，第 $i$ 道单选题有 $a_i$ 个选项，这 $a_i$ 个选项编号是 $1,2,3,\ldots,a_i$，每个选项成为正确答案的概率都是相等的。

lc 采取的策略是每道题目随机写上 $1 \sim a_i$ 的某个数作为答案选项，他用不了多少时间就能期望做对 $\sum_{i=1}^n \frac{1}{a_i}$ 道题目。gx 则是认认真真地做完了这 $n$ 道题目，可是等他做完的时候时间也所剩无几了，于是他匆忙地把答案抄到答题纸上，没想到抄错位了：第 $i$ 道题目的答案抄到了答题纸上的第 $i+1$ 道题目的位置上，特别地，第 $n$ 道题目的答案抄到了第 $1$ 道题目的位置上。

现在 gx 已经走出考场没法改了，不过他还是想知道自己期望能做对几道题目，这样他就知道会不会被 lc 鄙视了。

我们假设 gx 没有做错任何题目，只是答案抄错位置了。

思路

$ a_i=a_{i+1} p_i=\frac{1}{a_i}$
$ a_i>a_{i+1} i+1答案在i范围内的概率为\frac{a_{i+1}}{a_i},正确的概率为\frac{1}{a_{i+1}},\frac{a_{i+1}}{a_i} \cdot \frac{1}{a_{i+1}}= \frac{1}{a_i}$
$ a_i<a_{i+1}, i答案在i+1范围内的概率为\frac{a_i}{a_{i+1}},正确概率为\frac{1}{a_i},总概率为\frac{1}{a_{i+1}} $

$ ans= \sum_{i=1}^N \frac{1}{max(a_i,a_{i+1})} $

  
int n,a[N],A,B,C;
void init(){
  scanf("%d%d%d%d%d", &n, &A, &B, &C, a + 1);
  for (int i = 2; i <= n; i++)
      a[i] = ((long long) a[i - 1] * A + B) % 100000001;
  for (int i = 1; i <= n; i++)
      a[i] = a[i] % C + 1;
}
void solve(){
  init();
  a[n+1]=a[1];
  double ans=0;
  for(int i=1;i<=n;i++)ans+=1.0/max(a[i],a[i+1]);
  cout<<setprecision(3)<<fixed<<ans<<"\n";
}

[ABC314E] Roulettes

有 $N$ 个数列，第 $i$ 个数列的中有 $P_i$ 个数，分别是 $S_{i,1},S_{i,2},\cdots,S_{i,P_i}$。

高桥每次可以选一个数列 $i$，付出 $C_i$ 的代价，得到从 $S_{i,1},S_{i,2},\cdots,S_{i,P_i}$ 中等概率随机的一个数的得分，每次选择时随机抽到哪个数与之前的选择无关。

现在他要得至少 $M$ 分，每一次他可以根据之前的结果决定选择哪个数列，求他得至少 $M$ 分需要的最小期望代价。输出与答案的相对误差或绝对误差不超过 $10^{-5}$ 则视为正确。

思路：

考虑逆推，$ dp_i表示已经选了i分，还需要m-i分的期望代价，显然dp_m=0 ,答案为dp_0$
易看出dp方程：$ dp_i=c_i+ \sum {j=1}^{P_i} \frac{dp{i+a_j}}{P_i} $

$ 注意a_j=0的情况，此时右边式子会出现dp_i要移项到左边，然后再除系数，可以发现此时c_i也带系数了，应该预处理的时候将0处理掉 $

  
void solve(){
  int n,m;
  cin>>n>>m;
  vector<double> a[n+1],c(n+1);
  for(int i=1;i<=n;i++){
      cin>>c[i];
      int x;
      cin>>x;
      int cnt=0;
      for(int j=1;j<=x;j++){
          int y;
          cin>>y;
          if(y>0)a[i].push_back(y);
          else cnt++;
      }
      c[i]=c[i]*x/(x-cnt);
  }
  vector<double> dp(m+1,0);
  for(int i=m-1;i>=0;i--){
      double ans=1e18;
      for(int j=1;j<=n;j++){
          double tmp=c[j],cnt=0;
          for(auto x:a[j]){
              cnt+=i+x>=m?0:dp[i+x];
          }
          cnt/=a[j].size();
          tmp+=cnt;
          ans=min(ans,tmp);
      }
      dp[i]=ans;
  }
  cout<<setprecision(5)<<fixed<<dp[0]<<"\n";
}

This post is licensed under CC BY 4.0 by the author.

状压dp

棋盘式

P1896互不侵犯

炮兵阵地

集合式

P2831愤怒的小鸟

P3869宝藏(bfs+状态压缩)

区间dp

能量项链

P1040加分二叉树

P5752棋盘分割(二维区间dp)

P4170涂色

P8675搭积木(前缀和+区间dp)

P1436棋盘分割

树形dp

树的最长路径

两次dfs做法(只适用于无负权边)

树形dp(最大次大值更新)

树的最长路径的应用

SP6717 two paths(最水的黑题)/弱化版:CF14D two paths

数位dp

技巧

迭代写法

windy数

恨7不成妻

P4999烦人的数学作业

P2657windy数

P4317花神的数论题(二进制数位dp)

P6218[USACO06NOV]Round Numbers S(二进制数位dp)

CF628D Magic Numbers

P4124 [CQOI2016]手机号码

CF855E(数位dp+状态压缩)

P3413萌数

斜率优化dp

P5785任务安排

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

P4027货币兑换

CF311B 小猫铲屎

总结

概率dp,期望dp

期望

[国家集训队] 单选错位

题目描述

思路

[ABC314E] Roulettes

Trending Tags