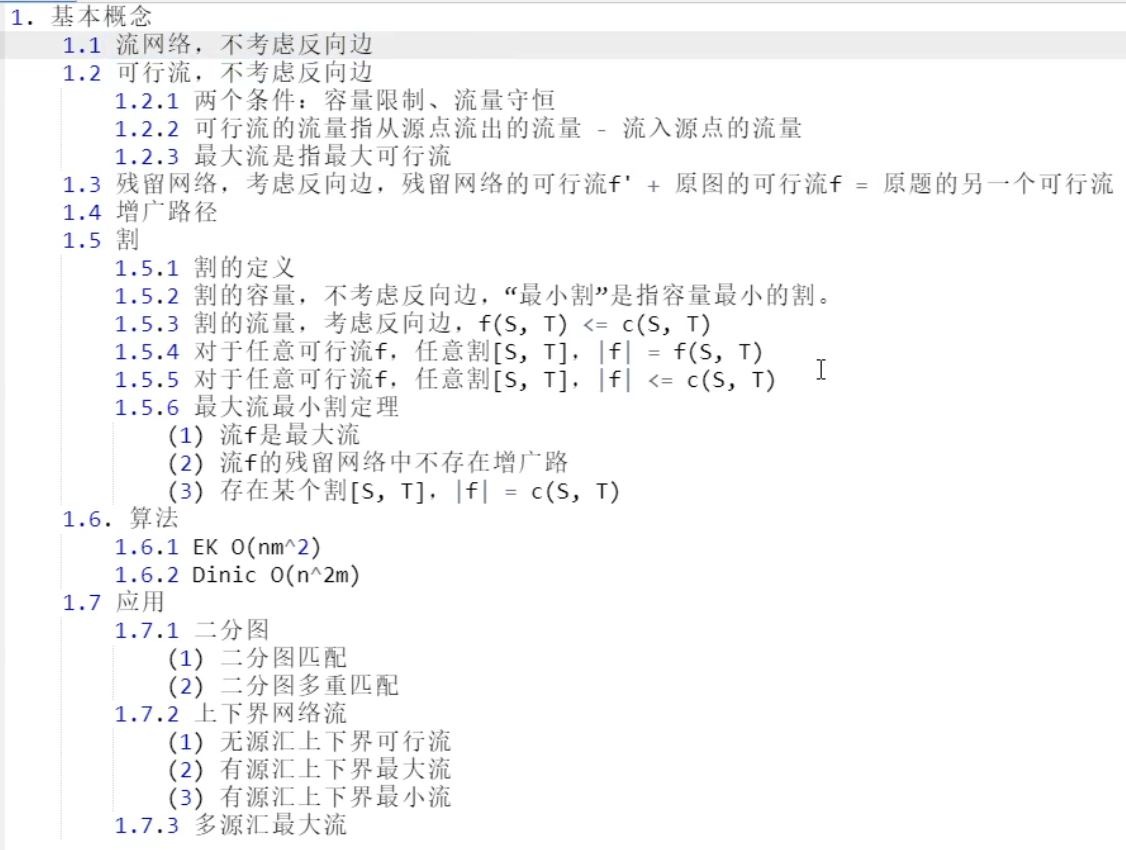
网络流
概念
- 残流网络
- $ c’(u,v)=c(u,v)-f(u,v) $
- $ c(v,u)=f(u,v) $(可以退回去)
$ f+f’ = f + f’ $ - 增广路径:沿着大于0的边能走到终点的路径
- 割的定义
- 将点集分成两部分:$ 源点集S和汇点集T ,称作割$
- 割的容量:$ c(S,T)= \sum_{u属于S} \sum_{v属于T} c(u,v) $
- $ 可行流f和割容量c(S,T),满足|f|<=c(S,T) 即最大流等于最小割$
Edmonds-Karps算法$ O(nm^2)(能处理10^3-10^4规模的网络) $
- bfs找增广路
- 更新残留网络(正向减去f,反向加f,总流加f)
- 用链式前向星存图,连续存正反边,则异或即为反边
模板
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
const int N=210,M=10010; int n,m,S,T;//S为源点,T为汇点 int e[M],h[N],ne[M],idx;//链式前向星 int f[M],d[N],pre[N];//f存流量,d存增广路的最小值,pre求前驱路径的idx void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;//反向流量初始为0 } bool bfs(){ queue<int> q; memset(vis,0,sizeof vis); q.push(S); vis[S]=1; d[S]=INF; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(!vis[v]&&f[i]){ vis[v]=1; d[v]=min(d[u],f[i]); pre[v]=i; if(v==T)return true; q.push(v); } } } return false; } int EK(){ int r=0; while(bfs()){ r+=d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=d[T],f[pre[i]^1]+=d[T]; } } return r; } void solve(){ cin>>n>>m>>S>>T; memset(h,-1,sizeof h); for(int i=1;i<=m;i++){ int u,v,w; cin>>u>>v>>w; add(u,v,w); } cout<<EK(); }
Dinic算法 $ O(n^2m)(能处理10^4-10^5规模的网络) $
- 对EK算法的优化,dfs将所有增广路同时遍历
- 因为可能有环,因此需要bfs预处理一遍深度,分层遍历
- 对于一个节点x,当它在DFS中走到了第i条弧时,前i−1条弧到汇点的流一定已经被流满而没有可行的路线了那么当下一次再访问x节点时,前i−1条就没有任何意义了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58
const int N=210,M=10010; int n,m,S,T;//S为源点,T为汇点 int e[M],h[N],ne[M],idx;//链式前向星 int f[M],d[N],cur[N];//f存流量,d存层数,cur为弧优化,表示当前从哪条节点开始搜 void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;//反向流量初始为0 } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v];//一开始所有边都可以搜 if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){//深搜,limit表示从源点流向u的最多能流的流,flow表示已经流向汇点多少流 if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){//flow<limit优化很重要,否则易tle int v=e[i]; cur[u]=i;//弧优化更新 if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1;//如果到达不了T,标记下次就不会走到 f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs()) while(flow=find(S,INF))r+=flow; return r; } void solve(){ cin>>n>>m>>S>>T; memset(h,-1,sizeof h); for(int i=1;i<=m;i++){ int u,v,w; cin>>u>>v>>w; add(u,v,w); } cout<<dinic(); }
网络流应用
$ 可行流<=>可行解 $
- 关键:建图
二分图匹配 $ O(m \sqrt n) $
- 将源点
S与左边点连一条边,右边点与汇点T连一条边,所有边的容量均为1 - 证明:显然满足容量限制和流量守恒
- 左边点如果被选,流入容量为
1,那么流出容量也只能是1即只能连一条边到右边点;右边点同理
- 左边点如果被选,流入容量为
- 最大流=最大二分图匹配
P2756 飞行员配对方案问题(二分图模板)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
const int N=210,M=10010; int n,m,S,T; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; q.push(S); memset(d,-1,sizeof d); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ cur[v]=h[v]; d[v]=d[u]+1; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ int v=e[i]; cur[u]=i; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ memset(h,-1,sizeof h); cin>>m>>n; S=0,T=n+1; for(int i=1;i<=m;i++)add(S,i,1); for(int i=m+1;i<=n;i++)add(i,T,1); int u,v; while(cin>>u>>v,u!=-1)add(u,v,1); cout<<dinic()<<"\n"; for(int i=0;i<idx;i+=2){ if(e[i]>m&&e[i]<=n&&!f[i]){ cout<<e[i^1]<<" "<<e[i]<<"\n"; } } }
P3254圆桌问题(类二分图匹配+最大流)
题意:
m个不同单位,派出r_i个代表,在n个圆桌聚餐,不希望看到同一单位在同一圆桌聚餐,求是否有方案数
圆桌不一定坐满 思路: - 网络流建图,源点向单位建边,容量为
r_i - 圆桌向汇点建边,容量为
c_i - 单位对每个圆桌建边,容量为
1 - 则每个单位流入
r_i,单位向一个圆桌只能流向一个人(满足题意) - 判断满流==人数
- 方案数枚举:
v为圆桌点就输出1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
const int N=500,M=100010; int n,m,S,T; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); d[S]=0,cur[S]=h[S]; q.push(S); while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ memset(h,-1,sizeof h); cin>>m>>n; S=0,T=m+n+1; int tot=0; for(int i=1;i<=m;i++){ int c; cin>>c; tot+=c; add(S,i,c); } for(int i=1;i<=n;i++){ int c; cin>>c; add(m+i,T,c); } for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++)add(i,m+j,1); } if(dinic()!=tot){ cout<<0; return; } cout<<1<<"\n"; for(int i=1;i<=m;i++){ for(int j=h[i];~j;j=ne[j]){ if(e[j]>m&&e[j]<=n+m&&!f[j]){ cout<<e[j]-m<<" "; } } cout<<"\n"; } }
无源汇上下界可行流
n个点,m条边有上下界满足流量守恒的可行方案
- $ 核心 (G,f)->(G’,f’) $
- $ c_L(u,v)<=f(u,v)<=c_H(u,v) 转化成0<=f(u,v)-c_L(u,v)<=c_H(u,v)-c_L(u,v) $
- $ c_{in}为少进的流量,c_{out}为少出的流量 $
- 源图流量守恒
- $ c_{in}>c_{out} ,即少进了c_{in}-c_{out}的流量,让源点S连一条边补上 $
- $ c_{in}<c_{out},向汇点连边 $
- 看方案是否有只需看是否满流
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71
const int N=500,M=100010; int n,m,S,T; int h[N],e[M],f[M],l[M],ne[M],idx; int d[N],cur[N],A[N];//A[i]表示i的少入还是少出 void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=d-c,l[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ int v=e[i]; cur[u]=i; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ cin>>n>>m; S=0,T=n+1; memset(h,-1,sizeof h); for(int i=1;i<=m;i++){ int a,b,c,d; cin>>a>>b>>c>>d; add(a,b,c,d); A[a]-=c,A[b]+=c; } int tot=0; for(int i=1;i<=n;i++){ if(A[i]>0)add(S,i,0,A[i]),tot+=A[i]; else add(i,T,0,-A[i]); } if(dinic()!=tot){ cout<<"NO\n"; return; } cout<<"YES\n"; for(int i=0;i<2*m;i+=2){ cout<<f[i^1]+l[i]<<"\n";//当前边满流等于残余网络的反向边流量 } }
有源汇上下界最大流
- $ 源网络s和t不满足流量守恒,将t连一条+∞的边到s,就变成无源汇上下界可行流,建新图 $
- $ 则对新图的s(原网络的源点)求到t(原网络的汇点)求增广路,没有则表示源网络最大流 $
- 证明:$ f <=> f’(s,t) $
- $ 源网络的f对应新网络的满流f’ $
$ f’+f’(s,t) 由于f’已满流,S不会有多余的流量流向s,剩余流量也进不去T,因此仍然是个满流即对应源网络的一个可行流 $ - $ 假设有一个f对应新网络的f’,另有一个新网络的流f_0’和f’_0(s,t) 则|f’-f’_0|,满流减满流就只剩下除S ,T的点可以考虑,对应f’_0(s,t) $
- $ 因此f<=>f’(s,t) $
$ 对于一个可行流f,新图存在一个满流f’与之对应,f’是一个定值,f’对应的s->t的流量记为f’_0(s,t)也是定值,要使f(s,t)= f’_0(s,t)+f_增(s,t) 最大就要增广(s,t) $
- 完整过程:
- t->s连边
- 无源上下界做法求最大流
- 删边t->s
- 残留网络求s->t最大流
- 若求的是最小流,则求t->s的最大流
- $ 最大流就是满流时t->s(中间节点流量守恒,等于s->t)的流量+增广流量 $
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71
int n,m,S,T,s,t; int h[N],e[M],f[M],ne[M],idx; int d[N],cur[N],A[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=d-c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); d[S]=0,cur[S]=h[S]; q.push(S); while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ cin>>n>>m>>s>>t; memset(h,-1,sizeof h); S=0,T=n+1; while(m--){ int a,b,c,d; cin>>a>>b>>c>>d; add(a,b,c,d); A[a]-=c,A[b]+=c; } int tot=0; for(int i=1;i<=n;i++){ if(A[i]>0)add(S,i,0,A[i]),tot+=A[i]; else add(i,T,0,-A[i]); } add(t,s,0,INF); if(dinic()!=tot){ cout<<"please go home to sleep\n"; return; } int res=f[idx-1];//t->s的流量 S=s,T=t; f[idx-2]=f[idx-1]=0;//流量为0,删边 cout<<res+dinic()<<"\n"; }
有源汇上下界最小流
与有源汇上下界最大流类似,只不过求的是反向增广流,最小流=原可行流-反向增广流
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
const int N=50010,M=(N+125003)*2; int n,m,S,T,s,t; int h[N],e[M],f[M],ne[M],idx; int d[N],cur[N],A[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=d-c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); d[S]=0,cur[S]=h[S]; q.push(S); while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ cin>>n>>m>>s>>t; memset(h,-1,sizeof h); S=0,T=n+1; while(m--){ int a,b,c,d; cin>>a>>b>>c>>d; add(a,b,c,d); A[a]-=c,A[b]+=c; } int tot=0; for(int i=1;i<=n;i++){ if(A[i]>0)add(S,i,0,A[i]),tot+=A[i]; else add(i,T,0,-A[i]); } add(t,s,0,INF); if(dinic()!=tot){ cout<<"please go home to sleep\n"; return; } int res=f[idx-1];//t->s的流量 S=t,T=s; f[idx-2]=f[idx-1]=0;//流量为0,删边 cout<<res-dinic()<<"\n"; }
多源汇最大流
建一个虚拟源点S和汇点T,S向原源点连∞边,汇点向T连∞边,跑dinic即可
最大流之关键边
在流网络中,只能改变一条边的容量,使最大流增加 关键边必定是满流的 $ 在G_f中存在S->u且v->T的>0的路径 $
模板POJ3204 Ikki’s Story I - Road Reconstruction
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
int n,m,S,T; int h[N],e[M],f[M],ne[M],idx; int d[N],cur[N]; bool vis_s[N],vis_t[N]; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); d[S]=0,cur[S]=h[S]; q.push(S); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void dfs(int u,bool st[],int t){ st[u]=1; for(int i=h[u];~i;i=ne[i]){ int j=i^t,v=e[i];//寻找路径,如果是从T开始找,那么应该判断反向边是否满流 if(f[j]&&!st[v])dfs(v,st,t); } } void solve(){ cin>>n>>m; memset(h,-1,sizeof h); S=0,T=n-1; for(int i=0;i<m;i++){ int a,b,c; cin>>a>>b>>c; add(a,b,c); } dinic(); dfs(S,vis_s,0); dfs(T,vis_t,1); int res=0; for(int i=0;i<2*m;i+=2){ if(!f[i]&&vis_s[e[i^1]]&&vis_t[e[i]]){ res++; } } cout<<res<<"\n"; }
最大流判定
P1674 [USACO05FEB] Secret Milking Machine G(秘密挤奶机,网络流+二分)
题意:
n个点,m条边,每条边(有长度)只能走一次,问从1-n能走t次的情况下,最长路最短 思路: 二分答案,将大于mid的边删掉,则题目转化为:
- 给定一张流网络,最大流是否大于等于
t1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
int n,m,S,T,t; int h[N],e[M],f[M],ne[M],w[M],idx; int d[N],cur[N]; void add(int a,int b,int c){ e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,w[idx]=c,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); d[S]=0,cur[S]=h[S]; q.push(S); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } bool check(int x){ for(int i=0;i<idx;i++){ if(w[i]>x)f[i]=0; else f[i]=1; } return dinic()>=t; } void solve(){ cin>>n>>m>>t; memset(h,-1,sizeof h); S=1,T=n; for(int i=0;i<m;i++){ int a,b,c; cin>>a>>b>>c; add(a,b,c); } int l=1,r=1e6; while(l<r){ int mid=l+r>>1; if(check(mid))r=mid; else l=mid+1; } cout<<l<<"\n"; }
P2754 [CTSC1999] 家园 / 星际转移问题(分层图建图)
- 题意
- 有
n个空间站,m搜太空船,地球编号0,月球为-1,太空船将周期性地停靠太空站,每转移一次耗费1个时间,问转移所有人的时间
- 有
- 思路
- 并查集判断是否能从地球到月球
- 网络流只与流量有关而与距离无关,要使二者产生关联应该建立分层图,每一天的每个太空站为一层,如下图所示(飞船相当于边)

- $ 第0天如果有飞船,则与S连容量为h_i(飞船限载人数)的边 $
- $ 所有天数的n+1的点向T连+∞的边 $
- $ 如果飞船能到下一个空间站,则向下一天的下一个站连边,容量为h_i $
- $ 飞船也可以停留一晚,向下一天的同一点连+∞的边 $
- 可以从0开始枚举天数,在增广路增加点继续增广
最大流拆点
P2891 [USACO07OPEN] Dining G
有食物饮料奶牛三种点,奶牛只吃一种食物和饮料(有些喜欢有些不喜欢,不喜欢则不连边),食物饮料只能用一次,问最多有几头牛能吃到食物喝饮料
- 类比二分图正常连边的话会有问题
- n(n>=2)种食物流进奶牛,n条边流向饮料,这是满足可行流的,但是不满足题意
- 将奶牛拆分成两个点,每次只允许一种食物通过奶牛即可

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
const int N=410,M=41000; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; int n,F,D,S,T; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ cin>>n>>F>>D; S=0,T=2*n+F+D+1; memset(h,-1,sizeof h); for(int i=1;i<=F;i++)add(S,n*2+i,1); for(int i=1;i<=D;i++)add(n*2+F+i,T,1); for(int i=1;i<=n;i++){ add(i,n+i,1); int a,b,x; cin>>a>>b; while(a--){ cin>>x; add(n*2+x,i,1); } while(b--){ cin>>x; add(n+i,n*2+F+x,1); } } cout<<dinic()<<"\n"; }
POJ3498/UVA12125 企鹅游行
题意:
一张二维图,给定n个点和企鹅的跳跃能力D,每个点上有ai只企鹅,bi次能用的起跳次数(超过就碎掉),问能否有一个点聚集所有的企鹅 思路:
- 初始有多少企鹅就从S连多少的边
- 枚举每个点能跳跃到的点,连正无穷边
- 枚举一个点当汇点跑dinic
- 还原流量$ f_i+=f_{i^1} f_{i^1}=0 $
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91
const int N=210,M=21000; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; int n,S,T; double D; PII p[N]; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } bool check(PII a,PII b){ double x=a.x-b.x; double y=a.y-b.y; return x*x+y*y<D+1e-8; } void solve(){ memset(h,-1,sizeof h); idx=0; cin>>n>>D; D*=D; S=0; int tot=0; for(int i=1;i<=n;i++){ cin>>p[i].x>>p[i].y; int a,b; cin>>a>>b; add(S,i,a),tot+=a; add(i,n+i,b); } for(int i=1;i<=n;i++){ for(int j=i+1;j<=n;j++){ if(check(p[i],p[j])){ add(n+i,j,INF); add(n+j,i,INF); } } } int cnt=0; for(int i=1;i<=n;i++){ T=i; for(int j=0;j<idx;j+=2){ f[j]+=f[j^1]; f[j^1]=0; } if(dinic()==tot){ cout<<i-1<<" "; cnt++; } } if(!cnt)cout<<"-1"; cout<<"\n"; }
SP4063/POJ1149 PIGS
题意:
有m个猪圈,n个顾客,每个顾客需要b只猪,顾客有猪圈的钥匙,每一个顾客来(按顺序)打开一些猪圈,拿走一些猪,然后可以重新分配开了的猪圈的猪,下一个顾客来之前把猪圈关上,问最多能卖多少只猪
思路:
- 还原流量$ f_i+=f_{i^1} f_{i^1}=0 $
- 如果没有重新分配的条件,则题目转化为两组点求最大流
- 如果没有顺序,那么从顾客反向连一条容量(为他能拿到所有的猪的数量)的边,求最大流
- 有顺序做法:
$ 假设\frac{\sum _{e∈c}w_e }{ C }>\lambda $ $ \sum _{e∈c}w_e> C \cdot \lambda 即\sum _{e∈c}w_e- C \cdot \lambda>0即\sum _{e∈c}(w_e- \lambda)>0 $ <亦是如此,因此可以二分- 这里的边割集可以是所有令
s,t断开的边加上若干条无关边(集合就与流网络的边割集不一样了,即可以选集合S,T的内部边)- 对于
w'[i]=w[i]-lambda,如果<=0则不管有没有关都选上,一定会让答案更小 - 对于所有
>0肯定是越少选越好,即不要选集合内部边,这就和流网络的集合对应上了,就可以用网络流来解1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82
const int N=105,M=805; const double eps=1e-8,inf=1e8; int n,m,S,T; int h[N],e[M],ne[M],w[M],idx; double f[M]; int d[N],hh,tt,q[N],cur[N]; void add(int a,int b,int c) { e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; } bool bfs() { memset(d,-1,sizeof d); d[S]=hh=tt=0; q[0]=S; cur[S]=h[S]; while(hh<=tt) { int x=q[hh++]; for(int i=h[x];~i;i=ne[i]) { int y=e[i]; if(d[y]==-1&&f[i]) { d[y]=d[x]+1; cur[y]=h[y]; if(y==T)return true; q[++tt]=y; } } } return false; } double dfs(int x,double limit) { if(x==T)return limit; double flow=0; for(int i=cur[x];~i&&flow<limit;i=ne[i]) { cur[x]=i; int y=e[i]; if(d[y]==d[x]+1&&f[i]) { double t=dfs(y,min(f[i],limit-flow)); if(!t)d[y]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } bool dinic(double x) { double res=0; for(int i=0;i<idx;i+=2) if(w[i]<=x)res+=w[i]-x,f[i]=f[i^1]=0; else f[i]=f[i^1]=w[i]-x; double flow=0; while(bfs())while((flow=dfs(S,inf))>0)res+=flow; return res<=0; } int main() { memset(h,-1,sizeof h); scanf("%d%d%d%d",&n,&m,&S,&T); for(int i=1;i<=m;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); add(x,y,z),add(y,x,z); } double l=1,r=1e7; while(fabs(r-l)>eps) { double mid=(l+r)/2; if(dinic(mid))r=mid; else l=mid; } printf("%.2lf",l); return 0; }
SP839 OPTM - Optimal Marks
给你一个无向图G(V,E)。 每个顶点都有一个int范围内的整数的标记。 不同的顶点可能有相同的标记。
- 对于
对于边(u,v),我们定义Cost(u,v)= mark [u] xor mark [v]。
现在我们知道某些节点的标记了。你需要确定其他节点的标记,以使边的总成本尽可能小。
如果有多解,请输出$ \sum mark_i $最小的方案。如果仍有多解,输出任意一个。
思路:
- 每一位互不影响,最终求和即可
- mark为
0/1,则可以划分0和1两个集合,转换为在该图求最小割容量(边权对应容量)- 对于初始为
0的点,与源点连无穷边,则它一定不会形成割边(无法满流),1的点向汇点连无穷边
- 对于初始为
- 然后如果问题求的最大值,应该是每一位
dinic(i)<<i,但是这题题意求所有点的对应数- 那么如果当前点存在增广路到达
T即d[i]!=-1,则加上当前数位值1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
const int N=510,M=(3000+N*2)*2; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N],p[N],ans[N]; int n,m,S,T; PII edges[3010]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=d,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void build(int k){ memset(h,-1,sizeof h); S=0,T=n+1; idx=0; for(int i=1;i<=n;i++){ if(p[i]>=0){ if(p[i]>>k&1)add(S,i,INF,0); else add(i,T,INF,0); } } for(int i=1;i<=m;i++)add(edges[i].x,edges[i].y,1,1); dinic(); for(int i=1;i<=n;i++){ if(d[i]!=-1)ans[i]|=(1ll<<k); } } void solve(){ memset(p,-1,sizeof p); memset(ans,0,sizeof ans); cin>>n>>m; for(int i=1;i<=m;i++)cin>>edges[i].x>>edges[i].y; int k; cin>>k; while(k--){ int x,y; cin>>x>>y; p[x]=y; } for(int i=0;i<31;i++)build(i); for(int i=1;i<=n;i++)cout<<ans[i]<<"\n"; }
最小割之最大权闭合图
闭合子图:一个点集,点的所有边都指向点的内部,然后包含这些点的所有边 最大权闭合图:集合内的点权总和最大
- 那么如果当前点存在增广路到达
- 建图,对于原图的边全用无穷边代替
- 对于点权大于等于0的点,与
S相连 - 对于点权小于0的点,与
T相连 - 边权均为绝对值
- 对于点权大于等于0的点,与
- 定义简单割:流网络中,割集中的边只会在与
S,T相连的边上- 证明:闭合子图<=>简单割
- 对于一个闭合子图的点集
v1来讲,对应于流网络的点集v1+S,那么点集的点不会走到另外一个集合,因此割边不会出现在原图的边中,即一个简单割 - 反之亦然
- 计算简单割的流量C(S,T),这里源点和汇点为
s,tS=v1+s,T=v2+t则有四种边v1->v2因为简单割割边不会出现在原图的边上,所以这种边不存在s->v2,存在v1->t,存在s->t,显然不存在
- $ 因此C(S,T)=C(s,v2)+C(v1,t)= \sum _{v∈v_2^+}w_v + \sum _{v∈v_1^-}(-w_v) $
- $ w_{v_1}= \sum _{v∈v_1^+} w_v - \sum _{v∈v_1^-} (-w_v) $
- $ 上诉两式相加得 C(S,T)+w_{v_1}=\sum _{v∈v_2^+}w_v+\sum _{v∈v_1^+} w_v= \sum _{为正数的点集}w_v $
- 那么右边为定值,要让
W_v最大即简单割最小 - 而简单割的割边一定不可能在原图边上(因为容量无穷),因此最小割也为简单割
- 因此求最小割,利用最终式子就能得到最大权子图了
P4174 [NOI2006] 最大获利
题意:
有n个通信站,m个公司,每个公司有三个参数a b c,如果建立了a,b两个通信站,则获利c元,建立通信站花费pi思路:
等价于向a,b连边,通信站设为负值,则转化为求最大权闭合子图1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82
#include<bits/stdc++.h> #define ll long long #define x first #define y second const int mod=19930726; const int INF=0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; const int N=55010,M=(N+5e4*2)*2; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; int n,m,S,T; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } void solve(){ cin>>n>>m; S=0,T=n+m+1; int tot=0; memset(h,-1,sizeof h); for(int i=1;i<=n;i++){ int p; cin>>p; add(m+i,T,p); } for(int i=1;i<=m;i++){ int a,b,c; cin>>a>>b>>c; add(S,i,c); tot+=c; add(i,m+a,INF); add(i,m+b,INF); } cout<<tot-dinic()<<"\n"; } signed main(){ cin.tie(0)->sync_with_stdio(0); int T=1; //cin>>T; while(T--)solve(); return 0; }
最小割之最大密度子图
在G(V,E)中选择一个V’和E’,使得对于任意一条边(E’内)的
u,v,都有u∈V' and v∈V'$ 最大化\frac{|E’|}{|V’|} $
- $ 令\frac{|E’|}{|V’|}=g,则按照01分数规划的思想,可以看出最大化|E’|-g|V’| $
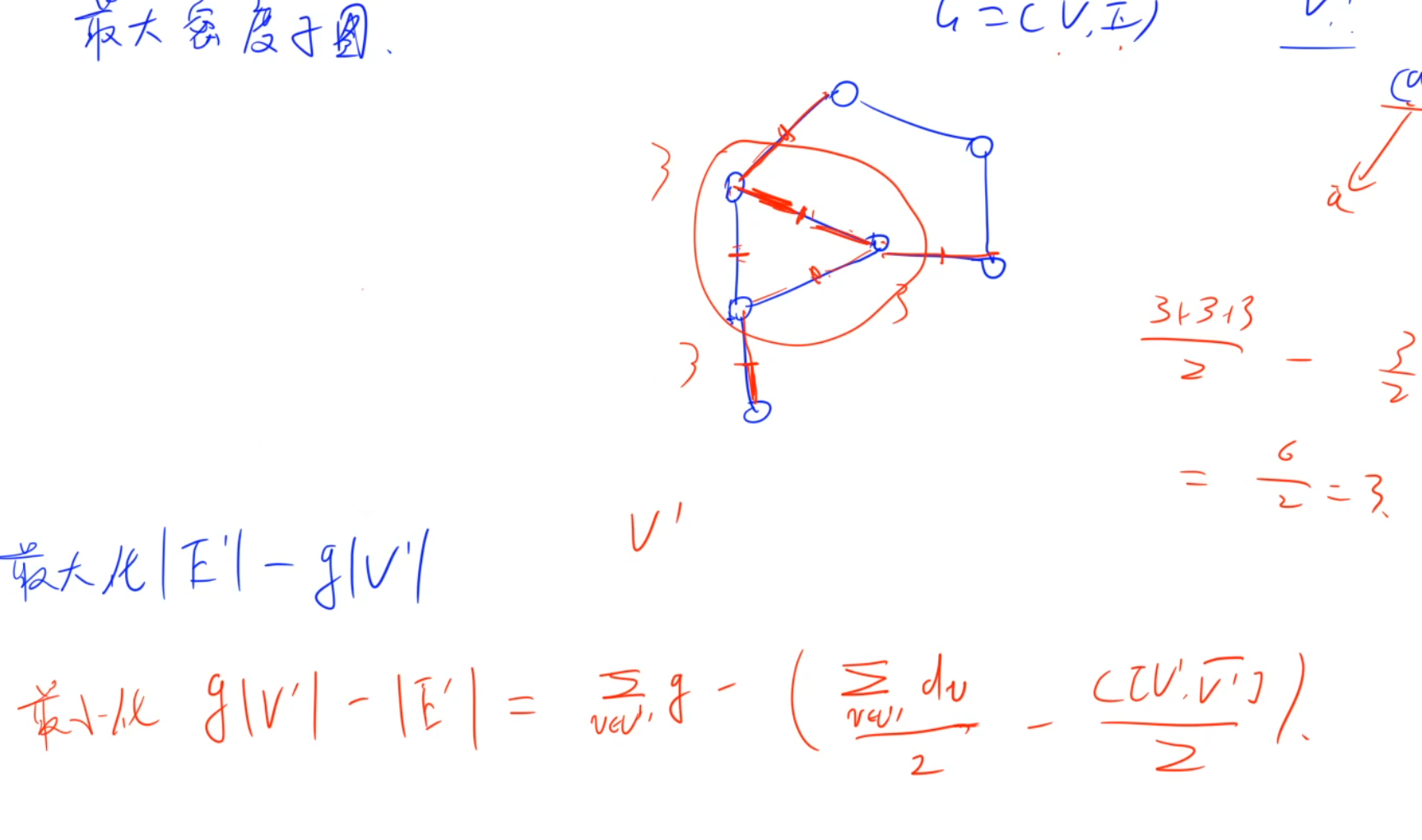
UVA1389Hard Life(黑题)
过于抽象,待补。。。
最小割之最小权点覆盖
最小权点覆盖,在图中选最小的点,能覆盖所有边 二分图中,最大匹配数=最小点覆盖数=n(若有权值则表示总权值)-最大独立集数(权值大于1仍成立)
- 建图,左边点向
S连容量为点权的边,右边向T连容量为点权的边,左右两边建无穷边 - 可证:点覆盖集<=>简单割
- 因此求流网络最小割就好
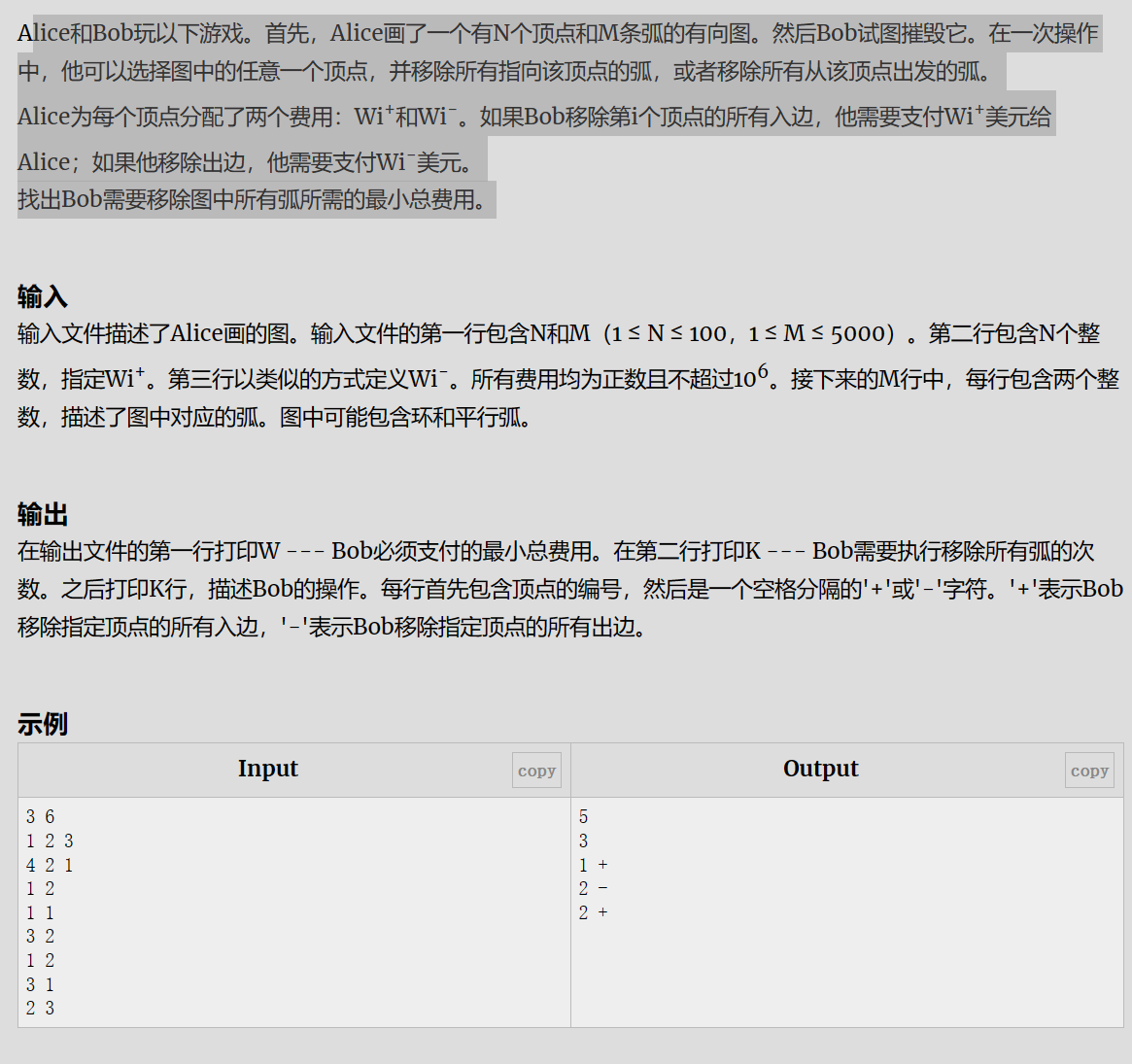
POJ2125 Destroying The Graph
- 找割边
- 从源点出发能到达的为
S,其余为T - 枚举所有正向边,若两点为
S->T即为割边最小割之最大权独立集
独立集:选出的点集中不存在边
- 从源点出发能到达的为
- 任意的点覆盖集的补集都是独立集
- $ 第i秒开始时,如果有宝石,捡起 $
- 偶数秒周围四格宝石消失
- 下一秒可以在上下左右或者原点位置
求最多拿宝石的数量 思路: - 分析可得只有偶数秒能取宝石
- 不可能同时拿走相邻宝石(可以发现为一个独立集)(合法方案=>独立集)
- 证明:独立集=>合法方案
- 可以通过停顿一次来重置奇偶性,来拿到所有独立集的点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
const int N=10010,M=60010; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; int n,m,S,T; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } int get(int x,int y){ return (x-1)*m+y; } void solve(){ cin>>n>>m; memset(h,-1,sizeof h); S=0,T=n*m+1; int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1}; int tot=0; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ int w; cin>>w; if(i+j&1){ add(S,get(i,j),w); for(int k=0;k<4;k++){ int x=i+dx[k],y=j+dy[k]; if(x>=1&&x<=n&&y>=1&&y<=m){ add(get(i,j),get(x,y),INF); } } } else add(get(i,j),T,w); tot+=w; } } cout<<tot-dinic()<<"\n"; }
SP300 CABLETV - Cable TV Network
题意:
给定一个n(n <= 50)个点的无向图,求它的点联通度。即最少删除多少个点,使得图不连通。 思路:
- 可以通过停顿一次来重置奇偶性,来拿到所有独立集的点
- 图不连通最开始的情况肯定是分成两个集合,因此想到最小割
- 题目是删点而不是删边,因此可以考虑拆点,一个点拆成入点和出点,容量为
1;原图边容量为无穷(这样就不会是割边,就不会拆边) - 定义简单割为割边只在点内部,易证:简单割<=>极小点集
- 枚举两个点当源点和汇点,跑最小割,所有最小割取min
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
const int N=110,M=52000; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; int n,m,S,T; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } int get(int x,int y){ return (x-1)*m+y; } void solve(){ while(cin>>n>>m){ memset(h,-1,sizeof h); idx=0; for(int i=0;i<n;i++)add(i,n+i,1); for(int i=1;i<=m;i++){ int u,v; scanf(" (%d,%d)",&u,&v); add(u+n,v,INF); add(v+n,u,INF); } int res=n; for(int i=0;i<n;i++){ for(int j=0;j<i;j++){ S=n+i,T=j; for(int k=0;k<idx;k+=2){ f[k]+=f[k^1]; f[k^1]=0; } res=min(res,dinic()); } } cout<<res<<"\n"; } }
P2762 太空飞行计划问题(最大权闭合子图)
题意:
有E={E1,E2,..}的实验,I={I1,I2,..}的仪器,实验可以获利,购买仪器需要钱,求最大净利润
思路:
裸的跑最大权闭合子图 - 找方案:
- S集合中所有的实验和仪器
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87
const int N=110,M=5200; int h[N],e[M],ne[M],f[M],idx; int d[N],cur[N]; int n,m,S,T; void add(int a,int b,int c){ e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; } bool bfs(){ queue<int> q; memset(d,-1,sizeof d); q.push(S); d[S]=0,cur[S]=h[S]; while(!q.empty()){ auto u=q.front(); q.pop(); for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(d[v]==-1&&f[i]){ d[v]=d[u]+1; cur[v]=h[v]; if(v==T)return true; q.push(v); } } } return false; } int find(int u,int limit){ if(u==T)return limit; int flow=0; for(int i=cur[u];~i&&flow<limit;i=ne[i]){ cur[u]=i; int v=e[i]; if(d[v]==d[u]+1&&f[i]){ int t=find(v,min(f[i],limit-flow)); if(!t)d[v]=-1; f[i]-=t,f[i^1]+=t,flow+=t; } } return flow; } int dinic(){ int r=0,flow; while(bfs())while(flow=find(S,INF))r+=flow; return r; } bool st[N]; void dfs(int u){ st[u]=true; for(int i=h[u];~i;i=ne[i]){ if(!st[e[i]]&&f[i])dfs(e[i]); } } void solve(){ cin>>m>>n; S=0,T=n+m+1; memset(h,-1,sizeof h); getchar(); int tot=0; for(int i=1;i<=m;i++){ int w,id; string line; getline(cin,line); stringstream ssin(line); ssin>>w; add(S,i,w); while(ssin>>id)add(i,m+id,INF); tot+=w; } for(int i=1;i<=n;i++){ int p; cin>>p; add(m+i,T,p); } int res=dinic(); dfs(S); for(int i=1;i<=m;i++){ if(st[i])cout<<i<<" "; } cout<<"\n"; for(int i=m+1;i<=m+n;i++){ if(st[i])cout<<i-m<<" "; } cout<<"\n"; cout<<tot-res<<"\n"; }
P3355 骑士共存问题(最大权独立集)
题意: 马(象棋走法)可以攻击八个方向的点,问在
n*n中能放多少个马
思路:
i+j分奇偶,就是一个最大权独立集
最小割求即可费用流(所有最大流中的费用最大值/最小值)
总费用等于流量*当前的边的费用
最小费用最大流
顾名思义,最大流中费用最小的
- S集合中所有的实验和仪器
- 将EK算法的bfs换成spfa,沿着最短路增广的费用一定更小
- 局限:无负权环
- 费用:w(u,v)=-w(v,u)
模板
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
const int N=5010,M=100010; int h[N],e[M],f[M],w[M],ne[M],idx; int d[N],mxf[N],pre[N];//d表示最短距离,mxf表示最大流,pre表示到i的边的编号 int n,m,S,T; bool vis[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++; } bool spfa(){ queue<int> q; memset(d,0x3f,sizeof d); memset(mxf,0,sizeof mxf); q.push(S); d[S]=0,mxf[S]=INF; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(f[i]&&d[v]>d[u]+w[i]){ d[v]=d[u]+w[i]; pre[v]=i; mxf[v]=min(f[i],mxf[u]); if(!vis[v]){ q.push(v); vis[v]=1; } } } } return mxf[T]>0; } void EK(int &flow,int &cost){ flow=cost=0; while(spfa()){ int t=mxf[T]; flow+=t,cost+=t*d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=t; f[pre[i]^1]+=t; } } } void solve(){ cin>>n>>m>>S>>T; memset(h,-1,sizeof h); for(int i=1;i<=m;i++){ int a,b,c,d; cin>>a>>b>>c>>d; add(a,b,c,d); } int flow,cost; EK(flow,cost); cout<<flow<<" "<<cost<<"\n"; }
P4015 运输问题(最小+最大)
思路:
- 运输方案<=>最大流
- 最小花费最大流
- 最大求法:
- 将所有费用取反
- 求最小费用,再取反
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
int h[N],e[M],f[M],w[M],ne[M],idx; int d[N],mxf[N],pre[N];//d表示最短距离,mxf表示最大流,pre表示到i的边的编号 int n,m,S,T; bool vis[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++; } bool spfa(){ queue<int> q; memset(d,0x3f,sizeof d); memset(mxf,0,sizeof mxf); q.push(S); d[S]=0,mxf[S]=INF; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(f[i]&&d[v]>d[u]+w[i]){ d[v]=d[u]+w[i]; pre[v]=i; mxf[v]=min(f[i],mxf[u]); if(!vis[v]){ q.push(v); vis[v]=1; } } } } return mxf[T]>0; } void EK(int &flow,int &cost){ flow=cost=0; while(spfa()){ int t=mxf[T]; flow+=t,cost+=t*d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=t; f[pre[i]^1]+=t; } } } void solve(){ cin>>m>>n; S=0,T=n+m+1; memset(h,-1,sizeof h); for(int i=1;i<=m;i++){ int x; cin>>x; add(S,i,x,0); } for(int i=1;i<=n;i++){ int x; cin>>x; add(m+i,T,x,0); } for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ int c; cin>>c; add(i,m+j,INF,c); } } int flow,cost; EK(flow,cost); cout<<cost<<"\n"; for(int i=0;i<idx;i+=2){ f[i]+=f[i^1],f[i^1]=0; w[i]=-w[i],w[i^1]=-w[i^1]; } EK(flow,cost); cout<<-cost; }
负载平衡问题
题意:
n个仓库组成一个环形,每个仓库可以向相邻点搬运货物,问所有仓库货物相等时,最少搬运量 思路:
- 求出平均值
x - 对于大于
x的仓库,说明货需要出去,连到源点 - 对于小于
x的仓库,说明货要进来,连到汇点 - 这样对于每个可行方案都会对应一个最大流
- 则求最小费用,一条边的费用为
11 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
const int N=110,M=1010; int h[N],e[M],f[M],w[M],ne[M],idx; int d[N],mxf[N],pre[N],s[N];//d表示最短距离,mxf表示最大流,pre表示到i的边的编号 int n,m,S,T; bool vis[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++; } bool spfa(){ queue<int> q; memset(d,0x3f,sizeof d); memset(mxf,0,sizeof mxf); q.push(S); d[S]=0,mxf[S]=INF; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(f[i]&&d[v]>d[u]+w[i]){ d[v]=d[u]+w[i]; pre[v]=i; mxf[v]=min(f[i],mxf[u]); if(!vis[v]){ q.push(v); vis[v]=1; } } } } return mxf[T]>0; } void EK(int &flow,int &cost){ flow=cost=0; while(spfa()){ int t=mxf[T]; flow+=t,cost+=t*d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=t; f[pre[i]^1]+=t; } } } void solve(){ cin>>n; S=0,T=n+1; int tot=0; memset(h,-1,sizeof h); for(int i=1;i<=n;i++){ cin>>s[i],tot+=s[i]; add(i,i>1?i-1:n,INF,1); add(i,i<n?i+1:1,INF,1); } tot/=n; for(int i=1;i<=n;i++){ if(s[i]>tot)add(S,i,s[i]-tot,0); else add(i,T,tot-s[i],0); } int flow,cost; EK(flow,cost); cout<<cost<<"\n"; }
分配问题(二分图最优匹配)
题意:
n个工作分配给n个人,第i个人做第j个工作的费用为C_{i,j}求最大和最小花费
思路: 二分图,跑模板数字梯形问题(拆点+费用流)
给定一个第一行为
m个点,有n行的类似杨辉三角的梯形,从第一行每个点往下走m条路经,求最大总和 分别求满足以下三个规则的最大值:- 从梯形的顶至底的 m 条路径互不相交;
- 从梯形的顶至底的 m 条路径仅在数字结点处相交;
- 从梯形的顶至底的 m 条路径允许在数字结点相交或边相交。 思路:
- 考虑规则1
- 对于每个点只能走一次,可以考虑拆点,入点和出点连容量为
1,费用为点数的边 - 最上面点连源点,容量为
1,费用为0 - 最下面连汇点,容量
1费用0 - 按题意每个点连容量
1费用0
- 对于每个点只能走一次,可以考虑拆点,入点和出点连容量为
- 对于规则2,两条路径可以交叉在一个点
- 即放开点内部的容量,连向其他的点容量仍为
1,因此保证从当前点到下一个点不会被走两次 - 往汇点的容量也放开,因为,多路径在最后一行汇集是合法的
- 即放开点内部的容量,连向其他的点容量仍为
- 对于规则3,在2的基础上
- 放开边的限制
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107
const int N=1100,M=4000; int h[N],e[M],f[M],w[M],ne[M],idx; int d[N],mxf[N],pre[N];//d表示最短距离,mxf表示最大流,pre表示到i的边的编号 int n,m,S,T; bool vis[N]; int id[40][40],C[40][40]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++; } bool spfa(){ queue<int> q; memset(d,0x3f,sizeof d); memset(mxf,0,sizeof mxf); q.push(S); d[S]=0,mxf[S]=INF; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(f[i]&&d[v]>d[u]+w[i]){ d[v]=d[u]+w[i]; pre[v]=i; mxf[v]=min(f[i],mxf[u]); if(!vis[v]){ q.push(v); vis[v]=1; } } } } return mxf[T]>0; } void EK(int &flow,int &cost){ flow=cost=0; while(spfa()){ int t=mxf[T]; flow+=t,cost+=t*d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=t; f[pre[i]^1]+=t; } } } void solve(){ cin>>m>>n; int cnt=0; S=++cnt; T=++cnt; for(int i=1;i<=n;i++){ for(int j=1;j<=m+i-1;j++){ id[i][j]=++cnt; cin>>C[i][j]; } } int flow,cost; //规则1 memset(h,-1,sizeof h); idx=0; for(int i=1;i<=n;i++){ for(int j=1;j<=m+i-1;j++){ add(id[i][j]*2,id[i][j]*2+1,1,-C[i][j]); if(i==1)add(S,id[i][j]*2,1,0); if(i==n)add(id[i][j]*2+1,T,1,0); if(i<n){ add(id[i][j]*2+1,id[i+1][j]*2,1,0); add(id[i][j]*2+1,id[i+1][j+1]*2,1,0); } } } EK(flow,cost); cout<<-cost<<"\n"; //规则2 memset(h,-1,sizeof h); idx=0; for(int i=1;i<=n;i++){ for(int j=1;j<=m+i-1;j++){ add(id[i][j]*2,id[i][j]*2+1,INF,-C[i][j]); if(i==1)add(S,id[i][j]*2,1,0); if(i==n)add(id[i][j]*2+1,T,1,0); if(i<n){ add(id[i][j]*2+1,id[i+1][j]*2,1,0); add(id[i][j]*2+1,id[i+1][j+1]*2,1,0); } } } EK(flow,cost); cout<<-cost<<"\n"; //规则3 memset(h,-1,sizeof h); idx=0; for(int i=1;i<=n;i++){ for(int j=1;j<=m+i-1;j++){ add(id[i][j]*2,id[i][j]*2+1,INF,-C[i][j]); if(i==1)add(S,id[i][j]*2,1,0); if(i==n)add(id[i][j]*2+1,T,INF,0); if(i<n){ add(id[i][j]*2+1,id[i+1][j]*2,INF,0); add(id[i][j]*2+1,id[i+1][j+1]*2,INF,0); } } } EK(flow,cost); cout<<-cost<<"\n"; }
费用流之网格数问题
P2045 方格取数加强版(K取方格数)
题意:
从(1,1)开始走,每次只能向右或向下走,走到(n,n),走k次,每个数只能取一次,求最大能取的值 思路:
- 放开边的限制
- 拆点,点权转边权,建容量为
1的费用为点权的边- 因为下一次仍能走这个点,所以还要建容量为无穷费用为
0的边
- 因为下一次仍能走这个点,所以还要建容量为无穷费用为
- 然后源点与(1,1),(n,n)与汇点,每个能走到的点连边,容量无穷费用
01 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
const int N=5010,M=20010; int h[N],e[M],f[M],w[M],ne[M],idx; int d[N],mxf[N],pre[N];//d表示最短距离,mxf表示最大流,pre表示到i的边的编号 int n,k,S,T; bool vis[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++; } bool spfa(){ queue<int> q; memset(d,0x3f,sizeof d); memset(mxf,0,sizeof mxf); q.push(S); d[S]=0,mxf[S]=INF; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(f[i]&&d[v]>d[u]+w[i]){ d[v]=d[u]+w[i]; pre[v]=i; mxf[v]=min(f[i],mxf[u]); if(!vis[v]){ q.push(v); vis[v]=1; } } } } return mxf[T]>0; } void EK(int &flow,int &cost){ flow=cost=0; while(spfa()){ int t=mxf[T]; flow+=t,cost+=t*d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=t; f[pre[i]^1]+=t; } } } int get(int x,int y,int t){ return (x-1)*n+y+t*n*n; } void solve(){ cin>>n>>k; S=0,T=n*n*2+1; memset(h,-1,sizeof h); add(S,get(1,1,0),k,0); add(get(n,n,1),T,k,0); for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ int c; cin>>c; add(get(i,j,0),get(i,j,1),1,-c); add(get(i,j,0),get(i,j,1),INF,0); if(i+1<=n)add(get(i,j,1),get(i+1,j,0),INF,0); if(j+1<=n)add(get(i,j,1),get(i,j+1,0),INF,0); } } int flow,cost; EK(flow,cost); cout<<-cost<<"\n"; }
P4012 深海机器人问题
与上题类似
P1251 餐巾计划问题
题目描述
一个餐厅在相继的 $N$ 天里,每天需用的餐巾数不尽相同。假设第 $i$ 天需要 $r_i$ 块餐巾($i = 1, 2, \dots, N$)。餐厅可以购买新的餐巾,每块餐巾的费用为 $p$ 分;或者把旧餐巾送到快洗部,洗一块需 $m$ 天,其费用为 $f$ 分;或者送到慢洗部,洗一块需 $n$ 天($n \gt m$),其费用为 $s$ 分($s \lt f$)。
每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。
试设计一个算法为餐厅合理地安排好 $N$ 天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。
输入格式
由标准输入提供输入数据。文件第 $1$ 行有 $1$ 个正整数 $N$,代表要安排餐巾使用计划的天数。
接下来的一行是餐厅在相继的 $N$ 天里,每天需用的餐巾数。
最后一行包含 $5$ 个正整数 $p, m, f, n, s$。$p$ 是每块新餐巾的费用;$m$ 是快洗部洗一块餐巾需用天数;$f$ 是快洗部洗一块餐巾需要的费用;$n$ 是慢洗部洗一块餐巾需用天数;$s$ 是慢洗部洗一块餐巾需要的费用。
输出格式
将餐厅在相继的 $N$ 天里使用餐巾的最小总花费输出。
样例 #1
样例输入 #1
1
2
3
3
1 7 5
11 2 2 3 1
样例输出 #1
1
134
提示
对于 $100 \%$ 的数据,$1 \le N \le 2 \times 10^3$,$1 \le r_i \le 10^7$,$1 \le p, f, s \le 10^4$。
思路
- 建图:
- 左边为用过的毛巾(与源点连),右边为需要的毛巾(与汇点连)
- 那么对于左边的毛巾
- 要么什么都不干,即流向下一天用过的毛巾
- 要么通过快洗机,流向
n天之后的需求毛巾 - 要么通过慢洗机,流向
m天之后的需求毛巾
- 对于右边毛巾,除了来自快洗和慢洗,还要与源点连边,表示购买的毛巾
- 那么流网络满流时,右边需求一定恰好满(因为源点流出去无穷量,但是源点流向用过的毛巾不一定满,它可以流向下一天用过最终被丢掉)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66
const int N=4010,M=(N+2000*4)*2; int h[N],e[M],f[M],w[M],ne[M],idx; int d[N],mxf[N],pre[N];//d表示最短距离,mxf表示最大流,pre表示到i的边的编号 int n,m,S,T; int p,x,xp,y,yp,r[N]; bool vis[N]; void add(int a,int b,int c,int d){ e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++; e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++; } bool spfa(){ queue<int> q; memset(d,0x3f,sizeof d); memset(mxf,0,sizeof mxf); q.push(S); d[S]=0,mxf[S]=INF; while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=h[u];~i;i=ne[i]){ int v=e[i]; if(f[i]&&d[v]>d[u]+w[i]){ d[v]=d[u]+w[i]; pre[v]=i; mxf[v]=min(f[i],mxf[u]); if(!vis[v]){ q.push(v); vis[v]=1; } } } } return mxf[T]>0; } void EK(int &flow,int &cost){ flow=cost=0; while(spfa()){ int t=mxf[T]; flow+=t,cost+=t*d[T]; for(int i=T;i!=S;i=e[pre[i]^1]){ f[pre[i]]-=t; f[pre[i]^1]+=t; } } } void solve(){ cin>>n; S=0,T=2*n+1; memset(h,-1,sizeof h); for(int i=1;i<=n;i++){ cin>>r[i]; } cin>>p>>x>>xp>>y>>yp; for(int i=1;i<=n;i++){ add(S,i,r[i],0); add(n+i,T,r[i],0); add(S,n+i,INF,p); if(i+1<=n)add(i,i+1,INF,0); if(i+x<=n)add(i,n+i+x,INF,xp); if(i+y<=n)add(i,n+i+y,INF,yp); } int flow,cost; EK(flow,cost); cout<<cost<<"\n"; }
类似问题
P2223 [HNOI2001] 软件开发
###