Post

最大子矩阵专题(dp、悬线法、障碍物法、单调栈)

Posted Updated
By 10 min read

悬线法

悬线法的适用范围是单调栈的子集。具体来说，悬线法可以应用于满足以下条件的题目：

  • 需要在扫描序列时维护单调的信息；
  • 可以使用单调栈解决；
  • 不需要在单调栈上二分。

    引入

    SP1805 HISTOGRA - Largest Rectangle in a Histogram

    11
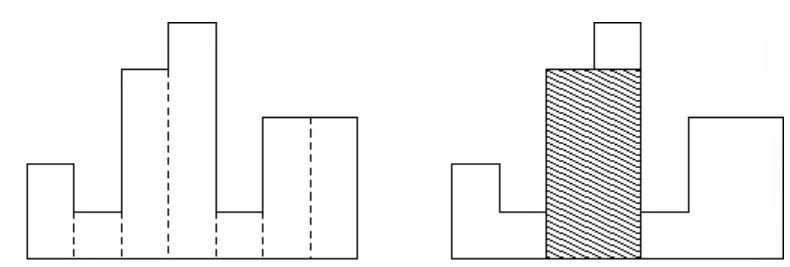
    如图所示，在一条水平线上有 n个宽为 1的矩形，求包含于些矩形的最大子矩形面积（图中的阴影部分的面积即所求答案）。
    显然，这是一道经典单调栈题目
    单调栈代码如下

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

    void solve(){
  ll n;
  while(cin>>n&&n!=0){
      stack<ll> st;
      vector<ll> a(n+1);
      for(int i=0;i<n;i++)cin>>a[i];
      a[n]=-1;//保证最后全部数出栈
      ll ans=0;
      for(int i=0;i<=n;i++){
          int x=-1;
          while(!st.empty()&&a[st.top()]>a[i]){
              x=st.top();
              st.pop();
              ans=max(ans,1ll*(i-x)*a[x]);
          }
          if(x!=-1){
              a[x]=a[i];
              st.push(x);//关键将准备要插入的块的长度延长至最后一个删除的块，才能确保答案正确
              continue;
          }
          else st.push(i);
      }
      cout<<ans<<"\n";
  }
}

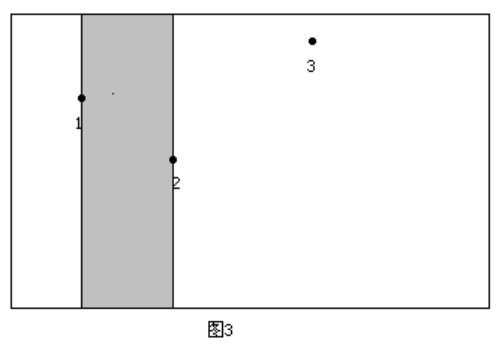
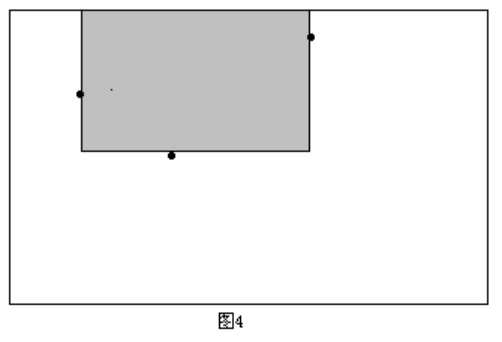
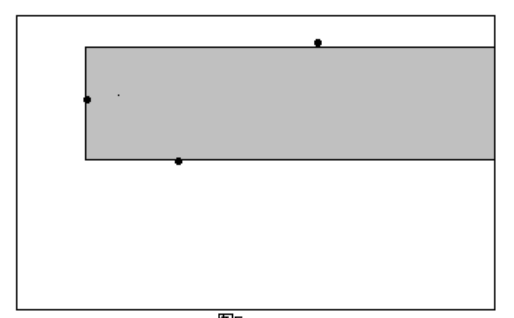
    将每一个高度看作一条悬线，可以左右移动，则该高度对应的长度即为左右可移动的长度
    定义 $l_i$ 为第 $i$ 个所能到达的左边界

  • $l_i=1$,说明到达最左端
  • $若a_i>a_{l_i-1}$,则说明不能扩展
  • 否则可以继续扩展,且 $l_i=l_{l_i-1}$
    右边界r同理
    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

    void solve(){
  ll n;
  while(cin>>n&&n!=0){
      vector<ll> a(n+1),l(n+1),r(n+1);
      iota(l.begin()+1,l.end(),1);
      iota(r.begin()+1,r.end(),1);
      for(int i=1;i<=n;i++)cin>>a[i];
      for(int i=2;i<=n;i++){
          while(l[i]>1&&a[i]<=a[l[i]-1])l[i]=l[l[i]-1];
      }
      for(int i=n-1;i>=1;i--){
          while(r[i]<n&&a[i]<=a[r[i]+1])r[i]=r[r[i]+1];
      }
      ll ans=0;
      for(int i=1;i<=n;i++){
          ans=max(ans,(r[i]-l[i]+1)*a[i]);
      }
      cout<<ans<<"\n";
  }
}

    UVA1619 感觉不错 Feel Good

    给出正整数 n和一个长度为n的数列a,求 $[l,r]$,满足：
    $ (\sum_{i=l}^{r}a_i) \cdot min_{i=l}^{r}a_i $

求最大值和相应的最小区间的两个端点 思路：枚举 $a_i$为最小值，看左边界和右边界，变成和上一题一样，再预处理前缀和即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

ll a[N],l[N],r[N],sum[N],n;
bool g=1;
void solve(){
    while(cin>>n){
        memset(a,-1,sizeof a);
        if(!g){
            cout<<"\n";
        }
        else g=0;
        for(int i=1;i<=n;i++){
            cin>>a[i];
            sum[i]=sum[i-1]+a[i];
            l[i]=r[i]=i;
        }
        for(int i=1;i<=n;i++){
            while(a[i]<=a[l[i]-1])l[i]=l[l[i]-1];
        }
        for(int i=n;i>=1;i--){
            while(a[i]<=a[r[i]+1])r[i]=r[r[i]+1];
        }
        ll ans=0;
        int ansl=1,ansr=1;
        for(int i=1;i<=n;i++){
            ll tmp=(sum[r[i]]-sum[l[i]-1])*a[i];
            if(ans<tmp){
                ans=tmp;
                ansl=l[i],ansr=r[i];
            }
            else if(ans==tmp&&ansr-ansl>r[i]-l[i])ansr=r[i],ansl=l[i];
        }
        cout<<ans<<"\n"<<ansl<<" "<<ansr<<"\n";
    }
}

最大子矩形 $O(NM)$

定义数组
$h_{i,j}$ 表示第j列以i为底所能到达的最大高度,即碰到障碍物或者上边界，全部初始化为1

$l_{i,j}$ 表示在第i行中j所能到达的最左边界，初始化为j

$r_{i,j}$同理

然后从左枚举更新l,从右枚举更新r,具体视题目而定

当 $a_{i,j} 和a_{i-1,j}$满足题目要求能存在于同一矩形时：

  • $ h_{i,j}=h_{i-1,j}+1 $
  • $ l_{i,j}=max(l_{i,j},l_{i-1,j})$
  • $ r_{i,j}=min(r_{i,j},r_{i-1,j})$

    P4147玉蟾宫

    题意：
    F表示空地，输出最大空地面积

以下写法仅限于矩形内只有一种元素,如下面的棋盘那道题这种写法就失效了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

void solve(){
    int n,m;
    cin>>n>>m;
    vector<vector<char>> ch(n+1,vector<char>(m+1));
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)cin>>ch[i][j];
    }
    vector<int> a(m+1),l(m+1),r(m+1);
    ll ans=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(ch[i][j]=='F')a[j]++;
            else a[j]=0;
            l[j]=r[j]=j;
        }
        for(int j=1;j<=m;j++){
            while(l[j]!=1&&a[j]<=a[l[j]-1])l[j]=l[l[j]-1];
        }
        for(int j=1;j<=m;j++){
            while(r[j]!=m&&a[j]<=a[r[j]+1])r[j]=r[r[j]+1];
        }
        for(int j=1;j<=m;j++){
            ans=max(ans,(ll)(r[j]-l[j]+1)*a[j]);
        }
    }
    cout<<ans*3;
}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

void solve(){
    int n,m;
    cin>>n>>m;
    vector<vector<char>> a(n+1,vector<char>(m+1));
    vector<vector<int>> h(n+1,vector<int>(m+1)),l(n+1,vector<int>(m+1)),r(n+1,vector<int>(m+1));
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
            h[i][j]=1;
            l[i][j]=r[i][j]=j;
        }
        for(int j=2;j<=m;j++){
            if(a[i][j]==a[i][j-1]&&a[i][j]=='F')l[i][j]=l[i][j-1];
        }
        for(int j=m-1;j>=1;j--){
            if(a[i][j]==a[i][j+1]&&a[i][j]=='F')r[i][j]=r[i][j+1];
        }
    }
    ll ans=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i>1){
                if(a[i][j]==a[i-1][j]&&a[i][j]=='F'){
                    h[i][j]=h[i-1][j]+1;
                    l[i][j]=max(l[i][j],l[i-1][j]);
                    r[i][j]=min(r[i][j],r[i-1][j]);
                }
            }
            if(a[i][j]=='F')ans=max(ans,(ll)(r[i][j]-l[i][j]+1)*h[i][j]);
        }
    }
    cout<<ans*3;
}

例题

P5943 [POI2002] 最大的园地

题意：
输出由0组成的最大面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

void solve(){
    int n;
    cin>>n;
    vector<vector<int>> a(n+1,vector<int>(n+1)),h(n+1,vector<int>(n+1)),l(n+1,vector<int>(n+1)),r(n+1,vector<int>(n+1));
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)cin>>a[i][j];
    }
    int ans=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            l[i][j]=r[i][j]=j;
            h[i][j]=1;
        }
        for(int j=2;j<=n;j++){
            if(a[i][j]==a[i][j-1]&&a[i][j]==0)l[i][j]=l[i][j-1];
        }
        for(int j=n-1;j>=1;j--){
            if(a[i][j]==a[i][j+1]&&a[i][j]==0)r[i][j]=r[i][j+1];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i>1&&a[i][j]==a[i-1][j]&&a[i][j]==0){
                l[i][j]=max(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
                h[i][j]=h[i-1][j]+1;
            }
            int x=r[i][j]-l[i][j]+1;
            if(a[i][j]==0)ans=max(ans,x*h[i][j]);
        }
    }
    cout<<ans;
}

P1169 [ZJOI2007] 棋盘制作

题意：
矩阵内只有黑和白，输出能分割的黑白相间的最大矩形和正方形
细节：只需将if条件从相等改成不等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

void solve(){
    int n,m;
    cin>>n>>m;
    vector<vector<int>> a(n+1,vector<int>(m+1)),h(n+1,vector<int>(m+1)),l(n+1,vector<int>(m+1)),r(n+1,vector<int>(m+1));
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)cin>>a[i][j];
    }
    int ans=0,res=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            l[i][j]=r[i][j]=j;
            h[i][j]=1;
        }
        for(int j=2;j<=m;j++){
            if(a[i][j]!=a[i][j-1])l[i][j]=l[i][j-1];
        }
        for(int j=m-1;j>=1;j--){
            if(a[i][j]!=a[i][j+1])r[i][j]=r[i][j+1];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i>1&&a[i][j]!=a[i-1][j]){
                l[i][j]=max(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
                h[i][j]=h[i-1][j]+1;
            }
            int x=r[i][j]-l[i][j]+1;
            int y=min(x,h[i][j]);
            ans=max(ans,x*h[i][j]);
            res=max(res,y*y);
        }
    }
    cout<<res<<"\n"<<ans;
}

P2701 [USACO5.3] 巨大的牛棚Big Barn

法一：普通dp做法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

void solve(){
    int n,m;
    cin>>n>>m;
    vector<vector<int>> dp(n+1,vector<int>(n+1,1));
    vector<vector<char>> ch(n+1,vector<char>(n+1,'.'));
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        ch[x][y]='#';
        dp[x][y]=0;
    }
    for(int i=1;i<=n;i++)dp[0][i]=dp[i][0]=0;
    int ans=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(ch[i][j]=='.'){
                dp[i][j]=max(min({dp[i-1][j],dp[i][j-1],dp[i-1][j-1]})+1,dp[i][j]);
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            ans=max(dp[i][j],ans);
        }
    }
    cout<<ans;
}

法二：悬线法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

void solve(){
    int n,m;
    cin>>n>>m;
    vector<int> a(n+1),l(n+1),r(n+1);
    vector<vector<char>> ch(n+1,vector<char>(n+1,'.'));
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        ch[x][y]='#';
    }
    int ans=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(ch[i][j]=='.')a[j]++;
            else a[j]=0;
            l[j]=r[j]=j;
        }
        for(int j=1;j<=n;j++){
            while(l[j]!=1&&a[j]<=a[l[j]-1])l[j]=l[l[j]-1];
        }
        for(int j=1;j<=n;j++){
            while(r[j]!=n&&a[j]<=a[r[j]+1])r[j]=r[r[j]+1];
        }
        for(int j=1;j<=n;j++){
            ans=max(ans,min(a[j],r[j]-l[j]+1));
        }
    }
    cout<<ans;
}

障碍物法 $O(T^2)$

此法适用于障碍物稀疏，而N和M较大时的情况

P1578 奶牛浴场

先看主要算法步骤：
11
11
11
有如下三种情况：

  • 左边界必定为障碍物
  • 右边界必定为障碍物
  • 左右边界为矩形边界
    可以加入四个点表示矩形的四个端点，然后按x从小到大排序，第一二种情况就可以$O(T^2)$枚举出来 第三种情况即按y排序，一长度为x的最大值n，另一长度就是两点y的差值
    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

    void solve(){
  int l,w,n;
  cin>>l>>w>>n;
  vector<PLL> a;
  for(int i=0;i<n;i++){
      int x,y;
      cin>>x>>y;
      a.emplace_back(x,y);
  }
  n+=4;
  a.emplace_back(0,0);
  a.emplace_back(0,w);
  a.emplace_back(l,0);
  a.emplace_back(l,w);
  sort(a.begin(),a.end(),[&](PLL x,PLL y){
      return x.x<y.x;
  });
  ll ans=0;
  for(int i=0;i<n;i++){
      ll x1=a[i].x,x2=a[i].x,y1=0,y2=w;
      for(int j=i+1;j<n;j++){
          x2=a[j].x;
          ans=max(ans,(x2-x1)*(y2-y1));
          if(a[j].y<a[i].y)y1=max(y1,a[j].y);
          else y2=min(y2,a[j].y);
      }
      x1=a[i].x,x2=a[i].x,y1=0,y2=w;
      for(int j=i-1;j>=0;j--){
          x2=a[j].x;
          ans=max(ans,(x1-x2)*(y2-y1));
          if(a[j].y<a[i].y)y1=max(y1,a[j].y);
          else y2=min(y2,a[j].y);
      }
  }
  sort(a.begin(),a.end(),[&](PLL x,PLL y){
      return x.y<y.y;
  });
  for(int i=0;i<n-1;i++)ans=max(ans,(a[i+1].y-a[i].y)*l);
  cout<<ans;
}

    P8404 [CCC2022 J5] Square Pool

    罗恩想在他的n×n 的正方形院子里建一个正方形游泳池，但他的院子里有T 棵树。你的任务是确定他可以建造的最大的方形游泳池的边长。
    思路：
    与上一题不同，上一题障碍物可以和边重合，这题不行
    因此要换个角度，注意到最大矩形边界要么与给定边界重合要么刚好被树挡住，因此向四个角的外面加4棵树
    假定左右边界是被树挡住，那么可以从左到右枚举，与上一题一样维护上下边界，如果上下边界小于左右则直接break，否则更新答案；同理再枚举一遍上下

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

    void solve(){
  int n;
  cin>>n;
  int t;
  cin>>t;
  vector<PLL> a;
  a.emplace_back(0,0);
  a.emplace_back(0,n+1);
  a.emplace_back(n+1,0);
  a.emplace_back(n+1,n+1);
  for(int i=0;i<t;i++){
      int x,y;
      cin>>x>>y;
      a.emplace_back(x,y);
  }
  t+=4;
  sort(a.begin(),a.end(),[&](PLL x,PLL y){
      return x.x==y.x?x.y<y.y:x.x<y.x;
  });
  ll ans=0;
  for(int i=0;i<t;i++){
      ll y1=1,y2=n;
      for(int j=i+1;j<t;j++){
          if(y2-y1+1<a[j].x-a[i].x-1)break;
          ans=max(ans,a[j].x-a[i].x-1);
          if(a[j].y<=a[i].y)y1=max(y1,a[j].y+1);
          else y2=min(y2,a[j].y-1);
      }
  }
  sort(a.begin(),a.end(),[&](PLL x,PLL y){
      return x.y==y.y?x.x<y.x:x.y<y.y;
  });
  for(int i=0;i<t;i++){
      ll x1=1,x2=n;
      for(int j=i+1;j<t;j++){
          if(x2-x1+1<a[j].y-a[i].y-1)break;
          ans=max(ans,a[j].y-a[i].y-1);
          if(a[j].x<=a[i].x)x1=max(x1,a[j].x+1);
          else x2=min(x2,a[j].x-1);
      }
  }
  cout<<ans;
}
算法, 最大子矩阵(dp、悬线法、障碍物法、单调栈)
dp 悬线法 单调栈 最大子矩阵
This post is licensed under CC BY 4.0 by the author.