大学物理笔记
振动
简谐振动
简谐振动特点:加速度与位移的大小x成正比,而方向相反
简谐运动方程: $ x=Acos( \omega t+ \psi )$ 以弹簧为例推导:
$ F=-kx =ma$
$ \frac{dx^{2}}{dt} =- \frac{k}{m} x =- \omega ^2 x$
求该二阶常系数齐次线性方程可得 $ x=Acos( \omega t+ \psi )$
三大表达式:
- $ x=Acos( \omega t+ \psi )$
- $ v= \frac{dx}{dt} =-A \omega sin( \omega t+ \psi )=A \omega cos( \omega t+ \psi + \frac{\pi}{2} ) $
- $ a=\frac{dv}{dt} =-A \omega^2 cos( \omega t+ \psi )=A \omega^2 cos( \omega t+ \psi +\pi) $
振幅,周期,频率,相位
振幅: $A=x_{max}$
弹簧振子周期: $T= \frac{2\pi}{\omega} =2 \pi \sqrt{ \frac{m}{k}}$
频率= $\frac{1}{T}$
圆频率:$ \omega $
周期和频率反应振动的快慢,仅与振动系统本身物理性质有关
相位:$\omega t+ \psi$
初相位: $ \psi$
常数 $A和 \psi$的确定
t=0时,$x_0=Acos \psi ,v_0=-A \omega sin \psi$
$ \frac{x_0^2}{A^2}=cos^2 \psi, \frac{v_0^2}{A^2 \omega^2}=sin^2 \psi $
解得:
$A= \sqrt{x_0^2+ \frac{v_0^2}{ \omega^2}}, tan \psi=\frac{-v_0}{ \omega x_0}$
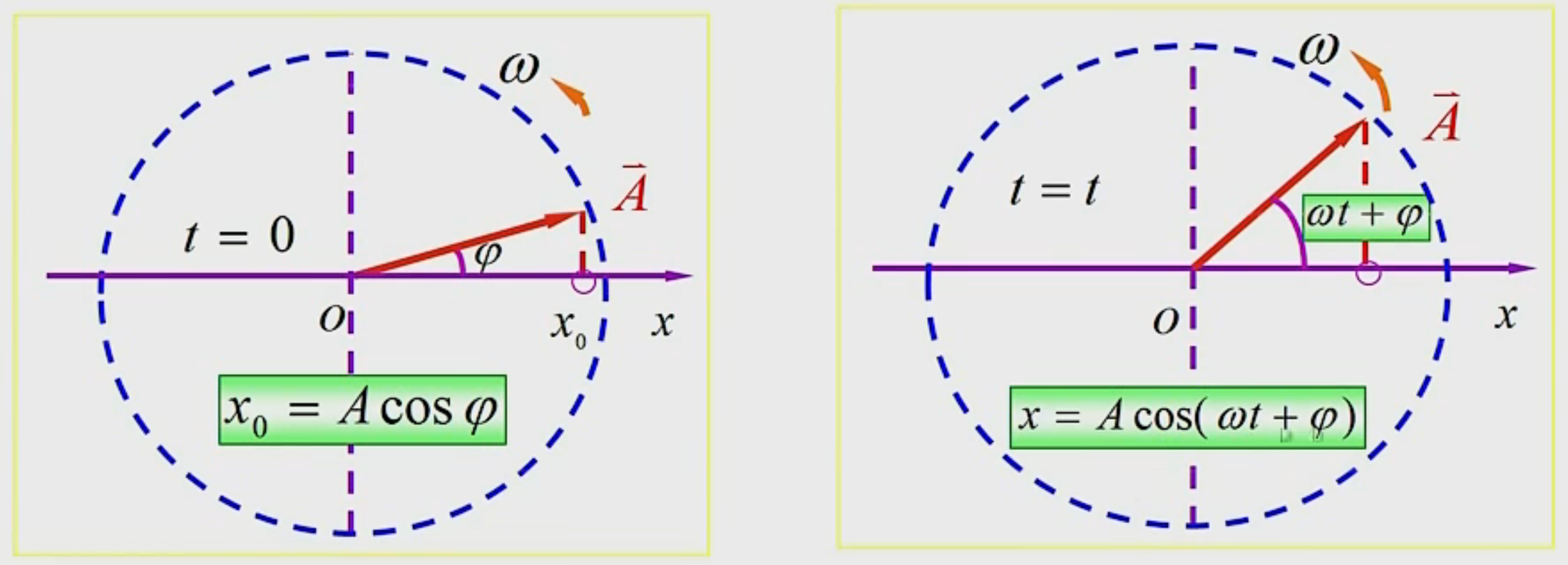
旋转矢量
简谐运动的表示方法
旋转矢量在x轴上的投影点的运动为简谐运动
相位差
同一简谐运动
$x_1=Acos( \omega t_1 + \psi) ,x_2=Acos( \omega t_2+ \psi)$
$ \Delta \psi =( \omega t_2 + \psi)-( \omega t_1 + \psi)$
$ \Delta t= \frac{\Delta \psi}{ \omega}$
同频率,但不同的简谐运动
$x_1=A_1cos( \omega t+ \psi _1),x_2=A_2cos( \omega t + \psi _2) $
$\Delta \psi =\psi _2- \psi _1 $ (初相位差)
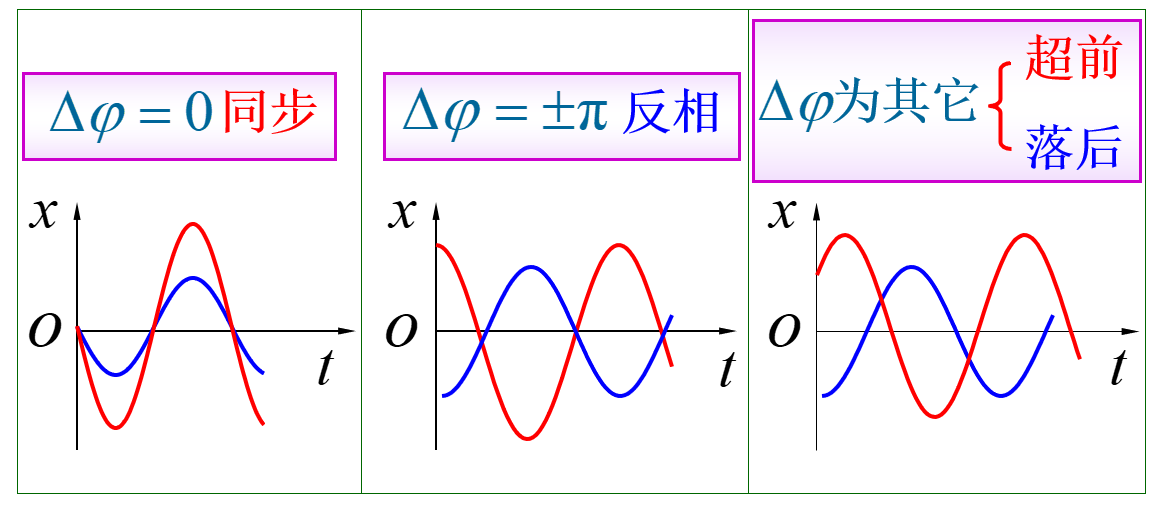
$ \Delta \psi= \psi _2 - \psi _1 $
大于0,2比1超前
小于0,2比1落后
单摆和复摆
单摆
单摆简谐运动方程: $ \theta =\theta _m cos( \omega t +\psi) $
$ M= \vec{r} \times \vec{F}=-mglsin \theta \approx -mgl \theta $
又因为 $ M=J \alpha =J \frac{d^2 \theta }{dt^2} ,J=ml^2 $
$ \frac{d^2 \theta }{dt^2}=- \frac{g}{l} \theta $
同理可得简谐运动公式,此时 $ \omega ^2= \frac{g}{l} $
周期 $ T=2 \pi \sqrt{ \frac{l}{g}}$
复摆
任意形状,小角度,无摩擦,自由摆动
可以用质心代替,类似成单摆,此时转动惯量J无法确定
$ \omega = \sqrt{ \frac{mgl}{J}}$
$ T=2 \pi \sqrt{ \frac{J}{mgl}}$
三种典型简谐运动频率和周期
|类型|角频率|周期| |——–|——–|———-| |弹簧振子| $ \omega = \sqrt{ \frac{k}{m}} $ | $ T=2 \pi \sqrt{ \frac{m}{k}} $ | |单摆| $ \omega = \sqrt{ \frac{g}{l}} $ | $ T=2 \pi \sqrt{ \frac{l}{g}} $ | |复摆| $ \omega = \sqrt{ \frac{mgl}{J}} $ | $ T=2 \pi \sqrt{ \frac{J}{mgl}} $ |
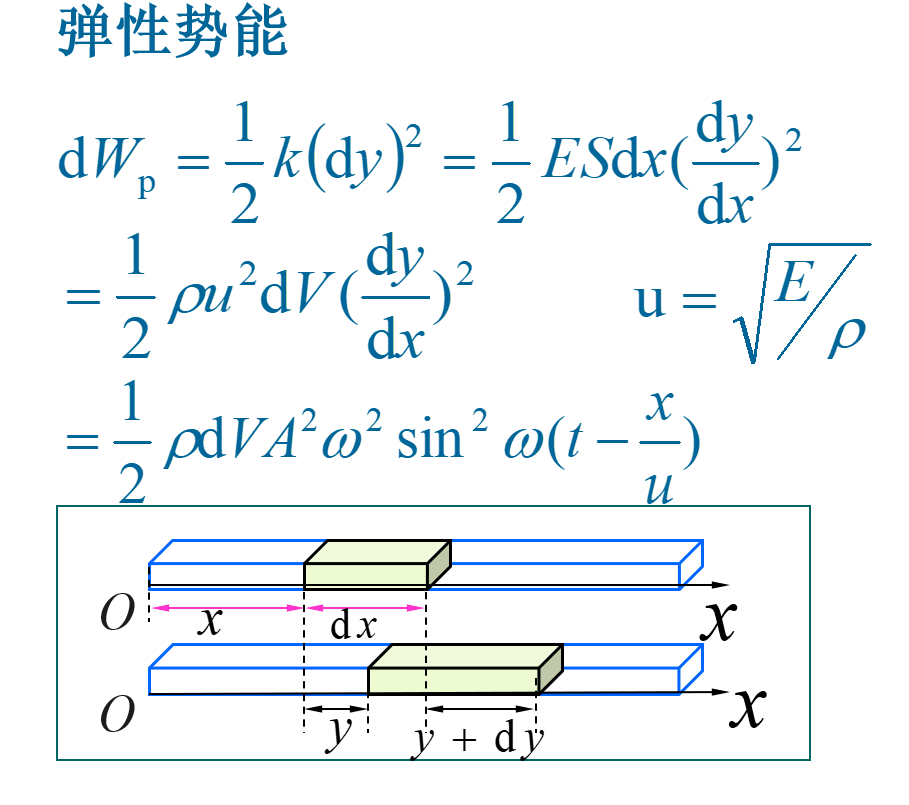
简谐运动的能量
以弹簧振子为例:运动产生的动能+弹簧形变产生的势能
动能
$E_k= \frac{1}{2}m \omega^2A^2sin^2( \omega t+ \psi)= \frac{1}{2}kA^2sin^2( \omega t + \psi)$
$E_{k_{max}} =\frac{1}{2}kA^2,E_{k_{min}}=0, \overline{E_k}= \frac{1}{4}kA^2 $
势能
$E_p= \frac{1}{2}kx^2= \frac{1}{2}kA^2cos^2( \omega t+ \psi)$
$E_{p_{max}},E_{p_{min}}, \overline{E_p}$ 和动能相同
平均动能,势能计算:对动能表达式从t到t+T对t积分,再除以T
机械能
$E= \frac{1}{2}kA^2= \frac{1}{2}m \omega^2A$
能量守恒推出简谐运动方程
$ \frac{d}{dt}( \frac{1}{2}mv^2+ \frac{1}{2}kx^2)=0 \to$
$ mv \frac{dv}{dt}+kx \frac{dx}{dt}=0 \to$
$ \frac{d^2x}{dt^2} +\frac{k}{m}x=0$
简谐运动的合成
两个同方向同频率的简谐运动的合成
分振动
$x_1=A_1cos( \omega t + \psi_1)$
$x_2=A_2cos( \omega t + \psi_2)$
合振动
$x=x_1+x_2$
$x=Acos( \omega t+ \psi)$
圆频率仍不变
$A= \sqrt{A_1^2+A_2^2+2A_1A_2cos( \psi _2- \psi _1)}$
$tan \psi = \frac{A_1sin \psi _1+A_2sin \psi _2}{A_1cos \psi _1+A_2cos \psi _2}$
两种特殊情况
1.若两分振动同相 $ \psi _2-\psi _1= \pm 2k \pi $,则 $A=A_1+A_2$,两分振动相互加强
2.若两分振动反相 $ \psi _2- \psi _1= \pm (2k+1) \pi$,则 $A=|A_1-A_2|$,两分振动相互减弱
两个相互垂直的同频率简谐运动的合成
分振动
$x=A_1cos( \omega t + \psi_1)$
$y=A_2cos( \omega t + \psi_2)$
合运动
轨迹方程: $ \frac{x^2}{A_1^2}+ \frac{y^2}{A_2^2}-2 \frac{x}{A_1} \frac{y}{A_2}cos(\psi _2 - \psi _1)=sin^2( \psi _2 -\psi _1)$


多个同方向同频率简谐振动的合成
仍为简谐振动, $ x=x_1+x_2+….+x_n $
两个同方向不同频率简谐运动的合成
拍:合振动振幅随周期性加强和减弱的现象
两个频率较大且相差极小的同方向谐振动合成形成拍
阻尼振动,受迫振动,共振
阻尼振动
由于克服阻力做功,振动系统能量不断减少,由于能量与振幅的二次方成正比,振幅逐渐减少,振幅随时间减少的振动叫做阻尼振动。
阻力
物体以不太大的速率在黏性介质中运动时,物体受到的阻力与其运动的速率成正比,即 $ F_r=-Cv$
$ -kx-Cv=ma $
$ m \frac{d^2x}{dt^2}+C \frac{dx}{dt}+kx=0 \to$ $ \frac{d^2x}{dt^2}+2 \delta \frac{dx}{dt} + \omega _0^2x=0$ (1)
固有角频率:$ \omega _0= \sqrt{ \frac{k}{m}}$
阻尼系数:$ \delta = \frac{C}{m} $
$ \to x=Ae^{ \delta t}cos( \omega t + \psi)$ (2)
把(2)代入(1)式得 $ \omega = \sqrt{ \omega _0^2- \delta^2}$
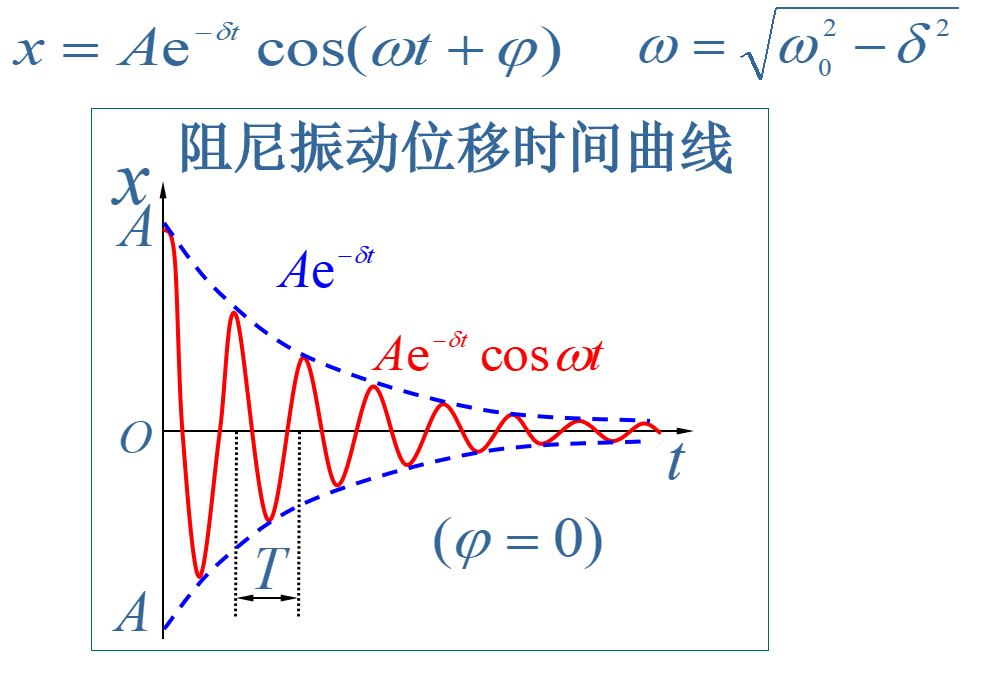
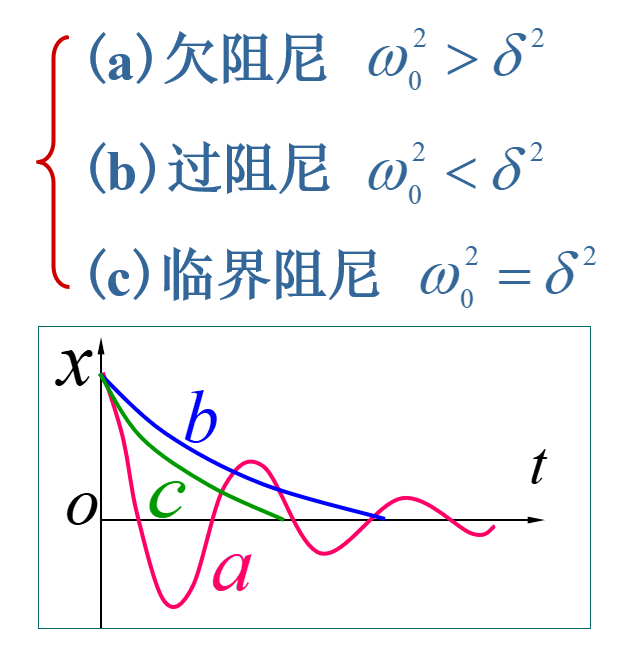
受迫振动
系统在周期性外力作用下进行的结果,叫做受迫振动。
受迫振动是由阻尼振动和简谐振动合成的
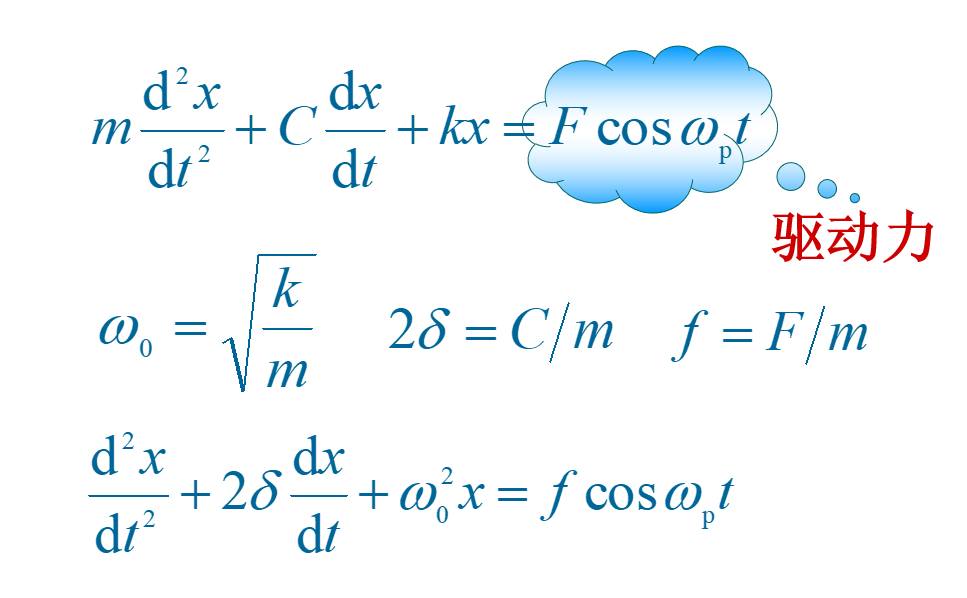
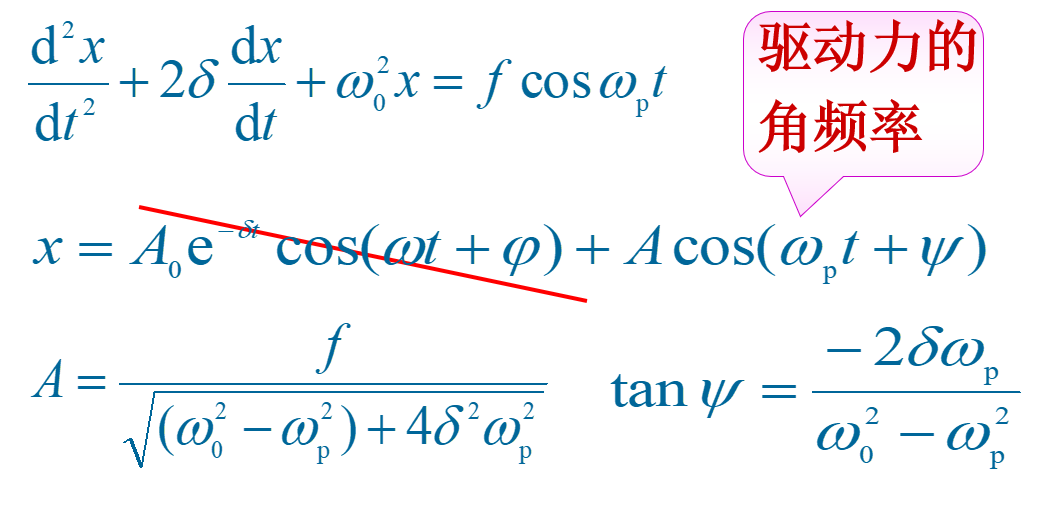
经过不太长的时间,阻尼振动衰减到可以忽略不计,振幅保持不变,受迫振动变为简谐振动
共振
驱动力的角频率为某一定值时,受迫振动的振幅达到极大的现象叫做共振,共振时的角频率叫做共振角频率。
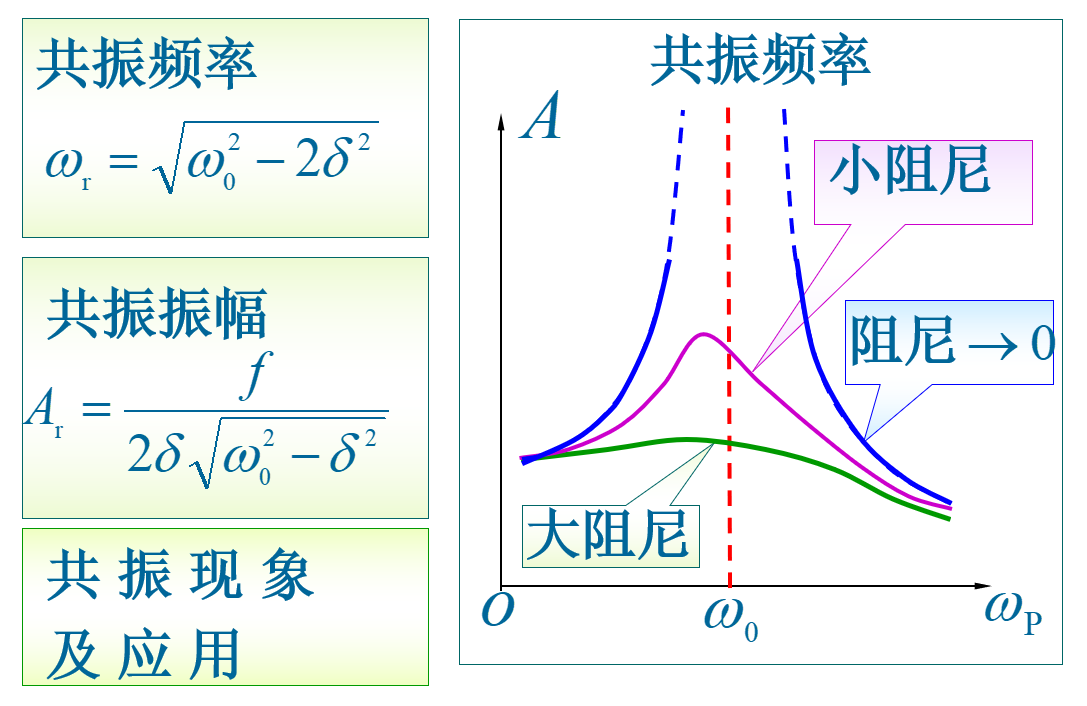
电磁振荡
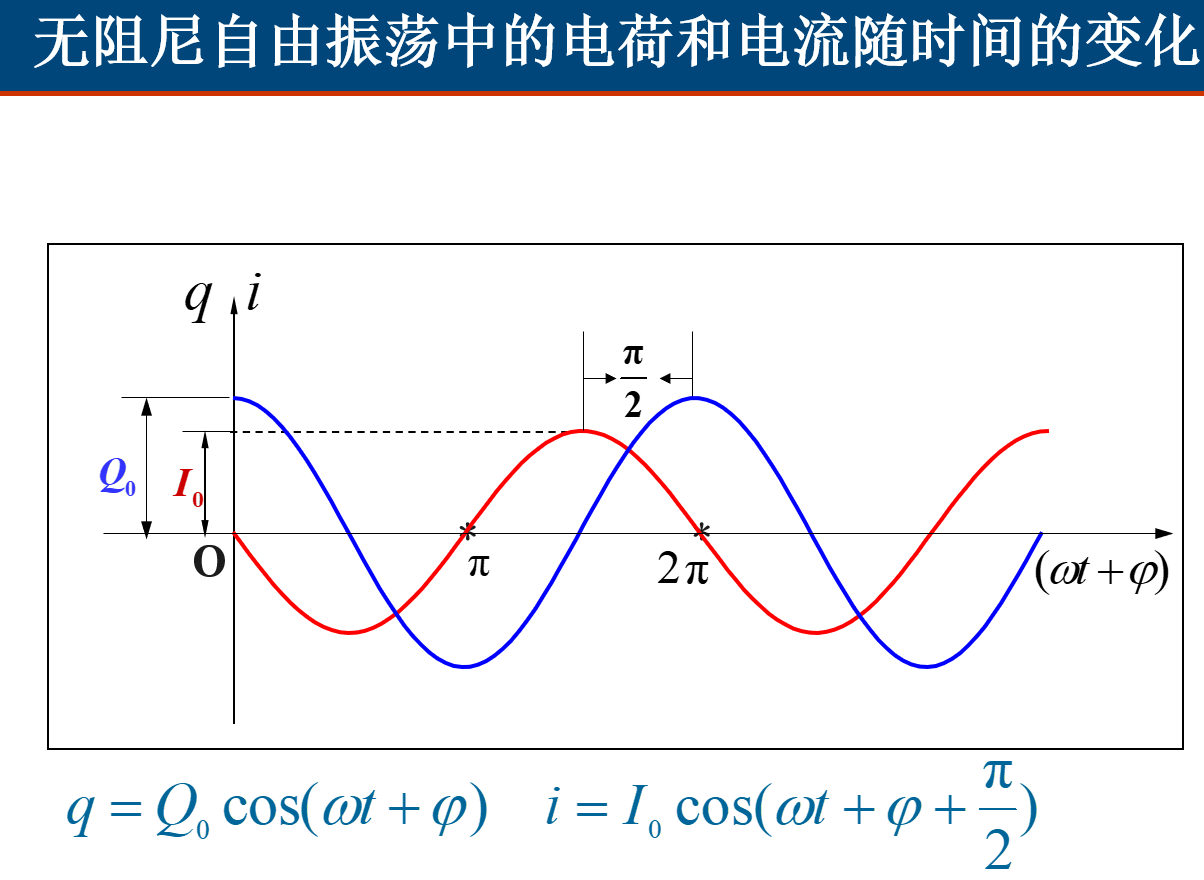
无阻尼自由电磁振荡(LC电磁振荡)
无阻尼电磁振荡能量
波动
机械波
机械波的形成
机械振动在连续介质中的传播称为机械波
形成条件:
- 波源
- 介质
横波与纵波
横波
特点:波传播方向上各点的振动方向与波传播方向垂直
纵波(疏密波)
如:弹簧波,声波
特点:质点的振动方向与波传播方向一致
结论
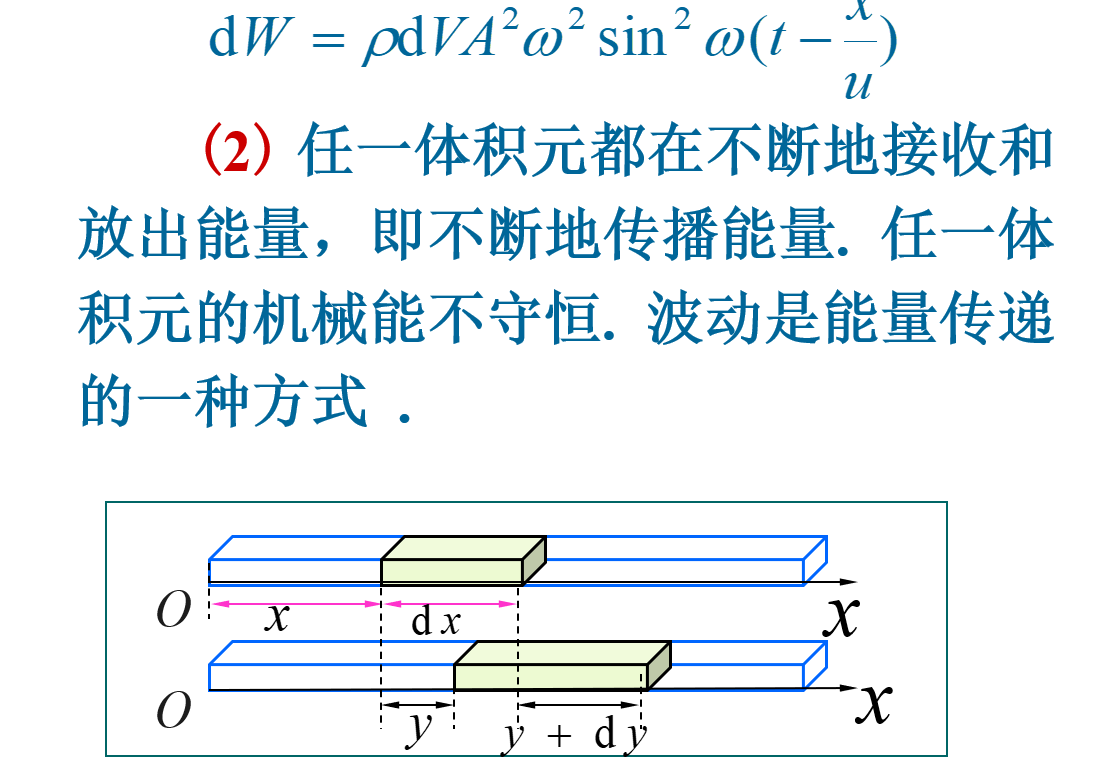
1.质元并未”随波逐流”,波的传播不是媒质质元的传播,而是振动状态的传播
2.”上游”的质元依次带动”下游”的质元振动
3.某时刻某质元的振动状态将在较晚时刻于”下游”某处出现–波是振动状态的传播
复杂波
例如:地震波、水波 特点:复杂波可分解为横波和纵波的合成
简谐波
波源及介质中各点均作简谐振动
两个概念
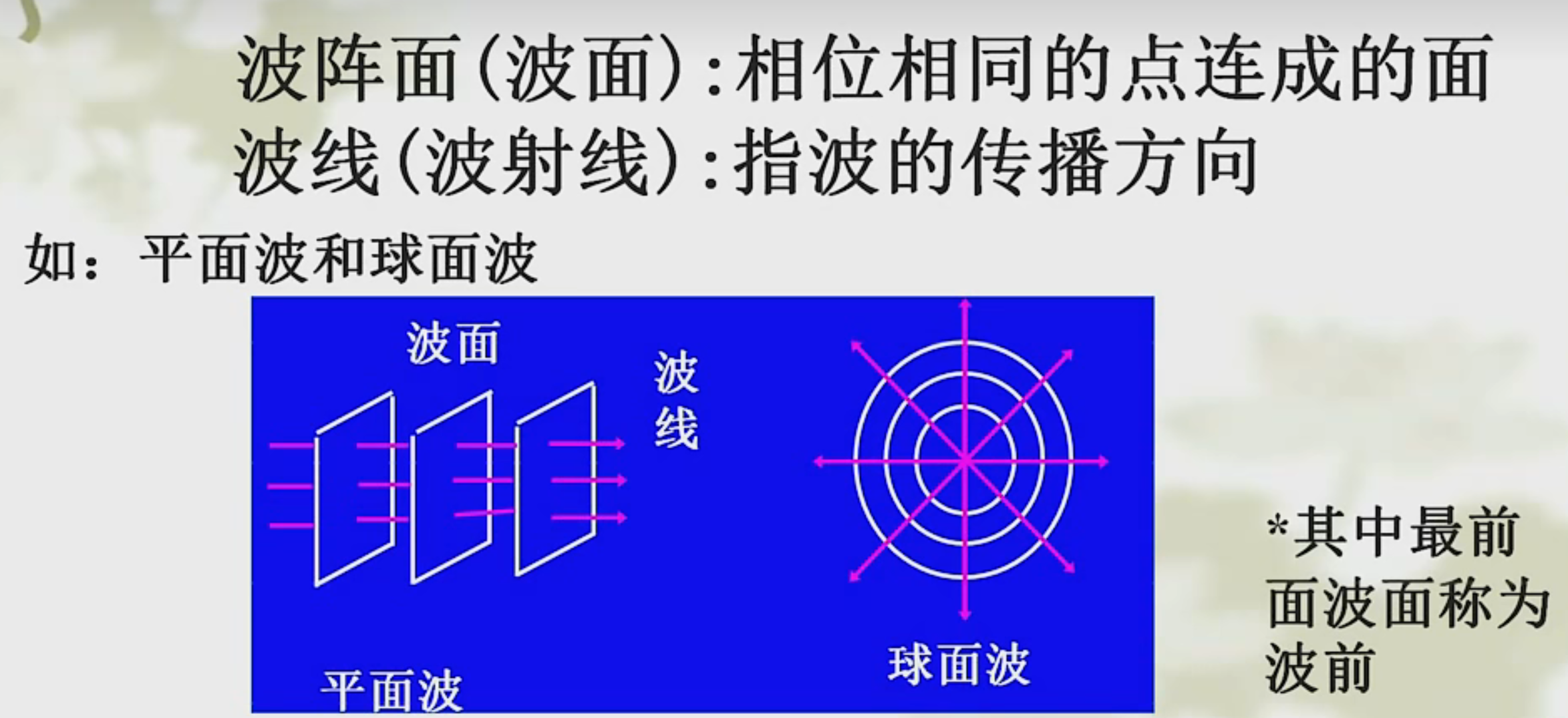
波线、波面、波前
波长、波的周期和频率、波速
波长 $ \lambda $ ,波速 $ \mu $,周期 $ T $ ,频率 $ \nu $ $ \mu = \frac{ \lambda }{T} = \lambda \nu$

周期或频率只决定于波源的振动
波速只决定于介质的性质
平面简谐波的波函数
平面简谐波的波函数
波函数的物理意义
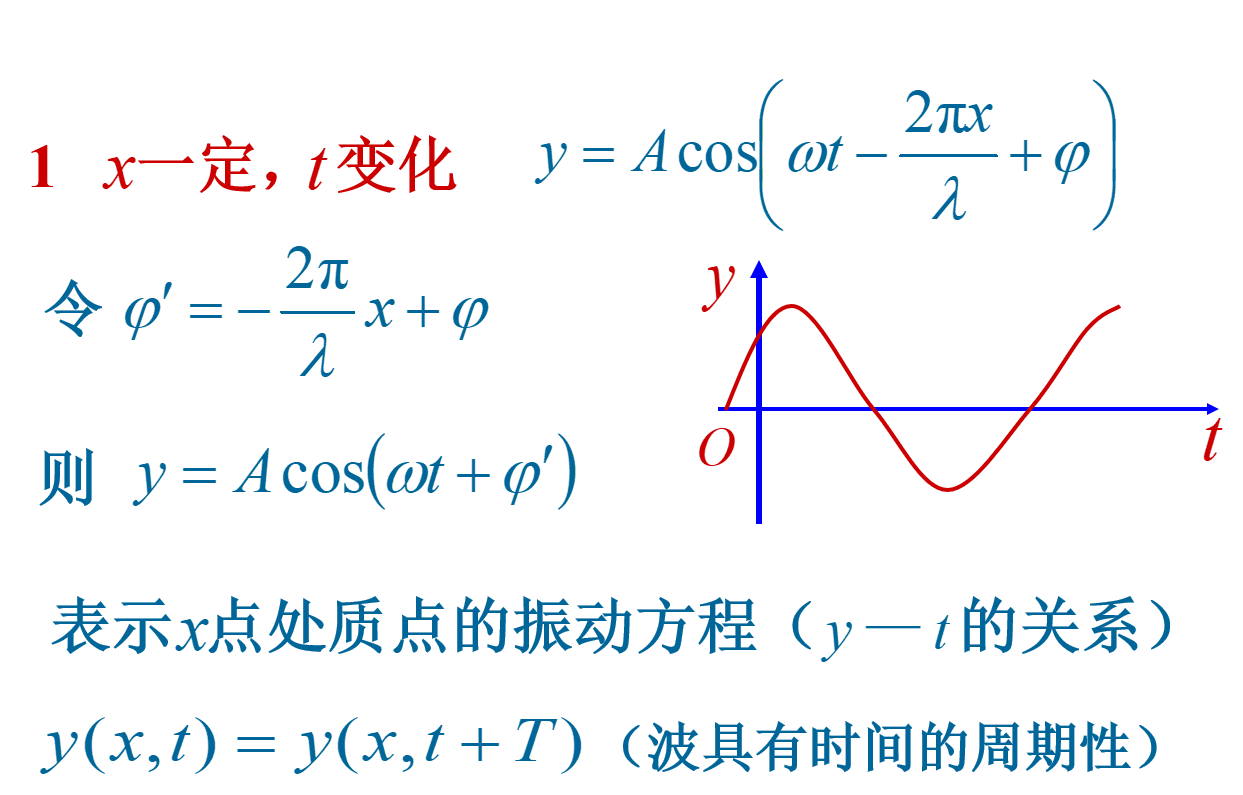
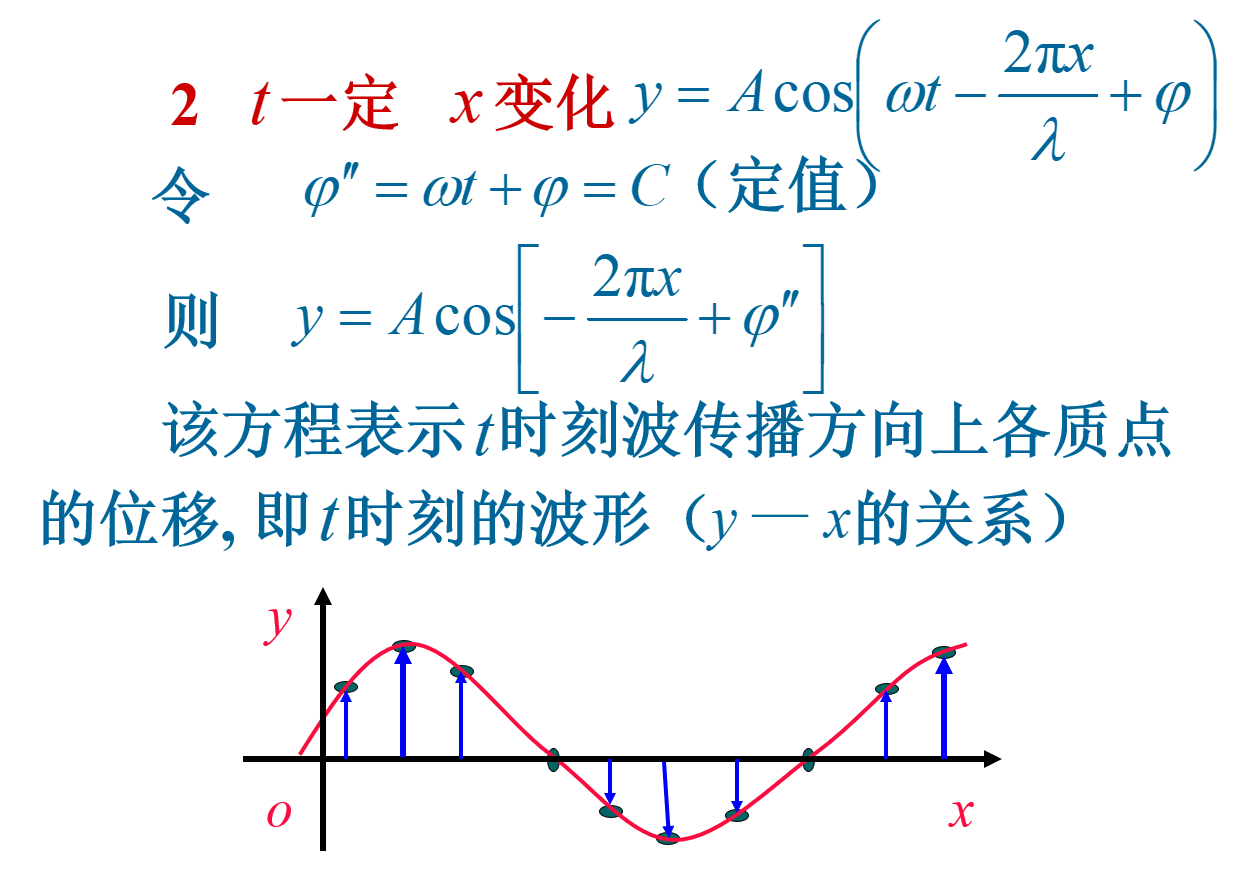
$ \omega = \frac{ 2 \pi }{T} =2 \pi \nu ,\mu = \lambda \nu = \frac{ \lambda }{T} \to y=Acos 2 \pi ( \frac{t}{T} - \frac{x}{ \lambda })$